পাইথনে ডাইনামিক প্রোগ্রামিং

ডাইনামিক প্রোগ্রামিং কোন অ্যালগরিদম নয়। মূলত এটা একটা কৌশল। নির্দিষ্ট কিছু সমস্যা, যে সমস্যা গুলোতে ছোট ছোট অংশ গুলোর সমাধানের পুনরাবৃত্তি ঘটে। ডাইনামিক প্রোগ্রামিং ব্যবহার করে সেই সমস্যা গুলো ইফিসিয়েন্টলি সমাধান করা যায়।

সাধারণত যে সমস্যা গুলো ডিভাইড এবং কনকার কৌশল ব্যবহার করে সমাধান করা যায়, সেগুলো ডিভাইড এবং কনকার কৌশলের সাথে ডাইনামিক প্রোগ্রামিং কৌশল ব্যবহার করলে দ্রুত সমাধানে পৌঁছা যায়। অ্যালগরিদমের ইফিশিয়েন্সি অনেকাংশে বাড়িয়ে দেয়। ডাইনামিক প্রোগ্রামিং কে বলা যায় মূলত অ্যালগরিদম অপটিমাইজেশনের একটা কৌশল।

ডাইনামিক প্রোগ্রামিং বুঝার জন্য রিকার্শন সম্পর্কে ধারণা থাকতে হবে। উদাহরণ হিসেবে আমরা ফিবোনাচি (Fibonacci) সিরিজ ব্যবহার করব। ফিবোনাচি সিরিজঃ

1, 1, 2, 3, 5, 8…

ফিবোনাচি সিরিজের প্রথম দুইটা সংখ্যা 1, 1। কেউ কেউ 0, 1 দিয়েও শুরু করে। এরপররের সংখ্যা গুলো হবে আগের সংখ্যা দুইটার যোগফল।

• তৃতীয় ফিবোনাচি সংখ্যা হচ্ছে আগের দুইটার যোগফল। এই ক্ষেত্রেঃ 1 + 1 = 2
• চতুর্থ ফিবোনাচি সংখ্যা হচ্ছেঃ 1 + 2 = 3
• পঞ্চম ফিবোনাচি সংখ্যা হচ্ছেঃ 2 + 3 = 5
• ষষ্ঠ ফিবোনাচি সংখ্যা হচ্ছেঃ 3 + 5 = 8
• তাহলে n তম ফিবোনাচি সংখ্যা হবেঃ fib(n − 1) + fib(n − 2)

যদি রিকার্শনের মাধ্যমে আমরা n তম ফিবোনাচি সংখ্যা বের করতে চাই, তাহলে প্রোগ্রামটা হবে এমনঃ

def fib(n):
    if (n == 1) or (n == 2):
        result = 1
    else:
        result = fib(n - 1) + fib(n - 2)
    return result

print(fib(5))

এই প্রোগ্রামটি fib(5) বের করার জন্য নিচের ধাপ গুলো অনুসরণ করবেঃ

উপরের ইমেজটি লক্ষ্য করি। যদি আমাদের fib(5) বের করতে হয়, তাহলে এর আগে fib(4) এবং fib(3)বের করতে হবে। আবার fib(3) বের করার জন্য আগে fib(2) এবং fib(1) বের করতে হবে।

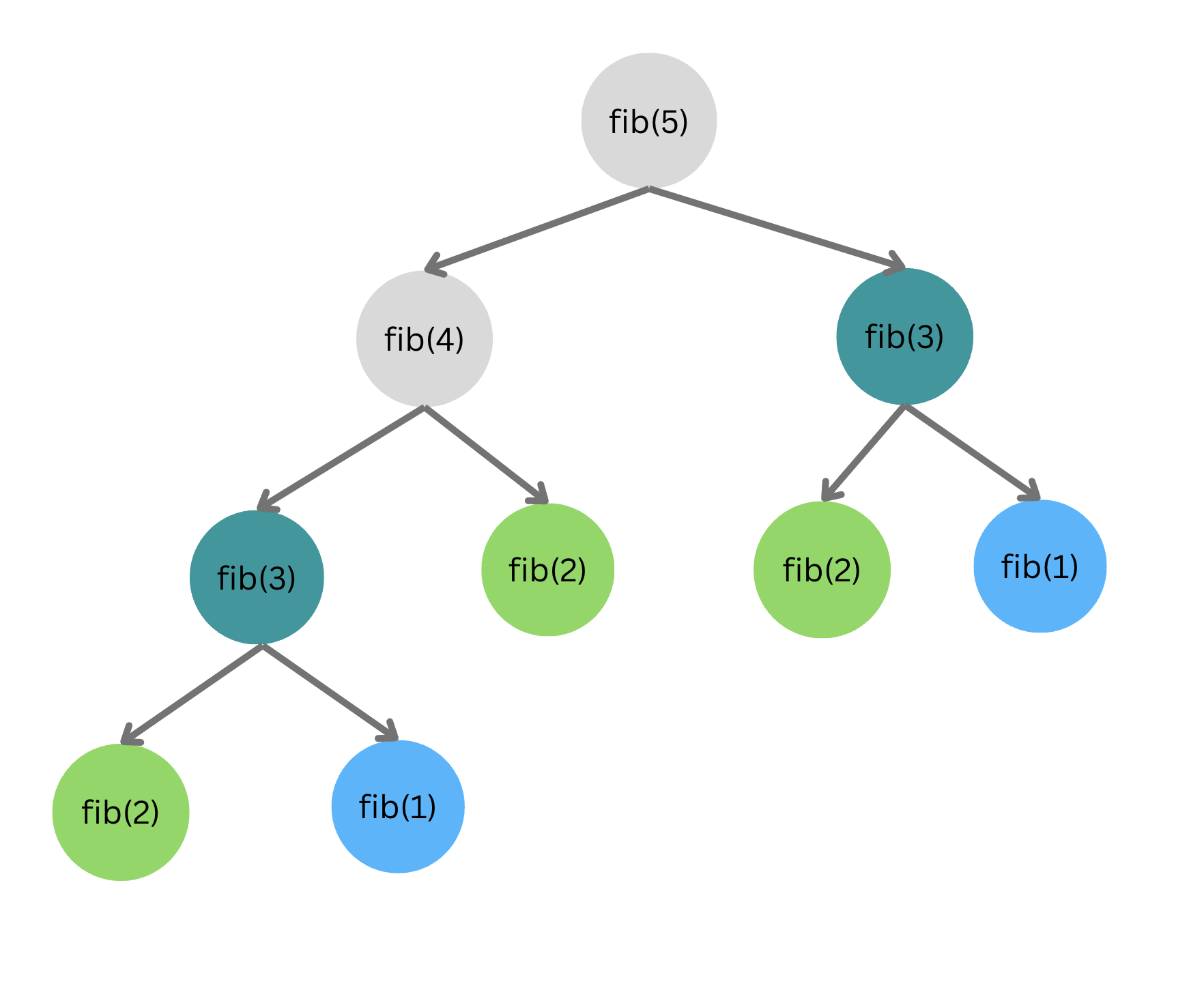
যদি আরো ভালো ভাবে লক্ষ্য করি, তাহলে দেখব শুধু মাত্র 5 তম ফিবোনাচি সংখ্যা বের করার জন্য fib(2) এর ভ্যালু বের করার জন্য 3 বার কল করতে হচ্ছে। fib(3) এবং fib(1) কে কল করতে হচ্ছে 2 বার।

৫ তম ফিবোনাচি সংখ্যা বের করার জন্য কম্পিউটার খুব একটা সময় নিবে না। কিন্তু যদি 50 বা 100 তম ফিবোনাচি সংখ্যা বের করতে যাই, দেখব ভালো কনফিগারেশনের কম্পিউটারও অনেক সময় নিচ্ছে। বিশ্বাস হচ্ছে না? উপরের প্রোগ্রামটি print(fib(50)) বা print(fib(100)) দিয়ে রান করে দেখতে পারেন।

দেখব অনেক দেরি করে আউটপুট দিচ্ছে। এই সমস্যা সমাধান করা যায় ডাইনামিক প্রোগ্রামিং ব্যবহার করে।

ডাইনামিক প্রোগ্রামিং এ যে সমাধানের পুনরাবৃত্তি ঘটে, সেগুলোকে প্রথমবার সমাধান করার পর সংরক্ষণ করে রাখে। দ্বিতীয় বা পরবর্তীতে ঐ সমস্যা সমাধান না করে আগে সংরক্ষণ করা সমাধানকে ব্যবহার করে। এই সংরক্ষণ করাকে বলা হয় Memoization। Memorization না।

এ জন্য আমরা একটা n+1 সাইজের লিস্ট নিব। যার মধ্যে আমরা ফিবোনাচি সংখ্যা বের করার পর সংরক্ষণ করে রাখব।

যেমন ঐ লিস্টের 1 নং ইনডেক্সে fib(1), 2 নং ইনডেক্সে fib(2)… এভাবে fib(n) এর মান গুলো সংরক্ষণ রাখব নিচের মত করেঃ

তবে প্রোগ্রামের শুরুতে n+1 সাইজের শূন্য লিস্ট নিব। যার মধ্যে None থাকবে শুরুতে। নিচের প্রোগ্রামটি দেখিঃ

def fib(n, memo):
    if memo[n] is not None:
        return memo[n]
    elif (n == 1) or (n == 2):
        result = 1
    else:
        result = fib(n - 1, memo) + fib(n - 2, memo)
    memo[n] = result
    return result


nth = 100
memo = [None] * (nth+1)
print(fib(nth, memo))

প্রথম প্রোগ্রামের সাথে এই প্রোগ্রামের সামান্য কিছু পার্থক্য রয়েছে। এখানে শুরুতেই if memo[n] is not None দিয়ে আমরা দেখে নিয়েছি যত তম ফিবোনাচি সংখ্যা বের করছি, তা memo লিস্টে আছে কিনা। যদি থাকে, এর মানে হচ্ছে ঐ n তম ফিবোনাচি ইতিমধ্যে বের করেছি আমরা। তাই ঐ ভ্যালুটি রিটার্ণ করেছি। যদি memo[n] যদি None হয়, তাহলে এর মানে হচ্ছে n তম ফিবোনাচি সংখ্যা বের করা হয়নি। তাই আগের মত এখানে ফিবোনাচি বের করার কোড লিকেছি। সবার শেষে এখানে রেজাল্ট রিটার্ণ করার আগে তা লিস্টে রেখে দিয়েছি।

এই প্রক্রিয়ায় ফিবোনাচি বের করার জন্য যেহেতু আমাদের একটা লিস্ট লাগবে, তাই কত তম ফিবোনাচি বের করব, তার পাশাপশি ঐ লিস্টটি প্যারামিটার হিসেবে পাস করেছি।

এখন প্রোগ্রামটি রান করে দেখব কত দ্রুত ফিবোনাচি সংখ্যা বের করে দিচ্ছে। উপরে যে পদ্ধতিতে ফিবোনাচি সংখ্যা বের করেছি, একে বলা হয় ডাইনামিক প্রোগ্রামিং এর টপ ডাউন পদ্ধতি।

ডাইনামিক প্রোগ্রামিং এর বটম আপ পদ্ধতি

উপরের প্রোগ্রামে আমরা রিকার্শন ব্যবহার করেছি। রিকার্শনের একটা সমস্যা হচ্ছে বড় কোন সংখ্যার জন্য ফিবোনাচি বের করতে গেলে RecursionError: maximum recursion depth exceeded in compariso দিবে। 1000 বা তার থেকে বড় তম ফিবোনাচি বের করার চেষ্টা করে দেখতে পারেন। পাইথনে অনেক গুলো রিকার্শন কল করলে এই ইরর দেয়।

রিকার্শন ব্যবহার না করে n তম ফিবোনাচি বের করার ক্ষেত্রে আমরা আরেকটা কৌশল ব্যবহার করতে পারি। যেমন উপরের প্রোগ্রামে 5th তম সংখ্যা বের করার জন্য প্রথমে fib(4) ও fib(3) কল করেছে। তারা আবার কল করেছে fib(2) এবং fib(1)। এর মানে হচ্ছে সবার আগে fib(1) বের করে memo লিস্টে রেখেছে। এরপর fib(2) বের করে memo লিস্টে রেখেছে। এখন আমরা রিকার্শন ব্যবহার না করেই সাধারণ ইটারেশন ব্যবহার করে এই সমস্যা সমাধান করতে পারি। প্রথমে fib(1) এবং fib(2) memo লিস্টে রাখব। এরপর fib(3) বের করে memo লিস্টে রাখব। এভাবে n তম সংখ্যা পর্যন্ত ইটারেশন করে ঐ লিস্টে রেখেই আমরা রেজাল্ট আউটপুট দিতে পারি। আর এই পদ্ধতিকে বলা হয় বটম আপ পদ্ধতি।

বটম আপ পদ্ধতিতে n ফিবোনাচি বের করার জন্য এভাবে কোড লিখতে পারিঃ

def fib(n):
    memo = [None] * (n + 1)
    if n == 1 or n == 2:
        return 1
    memo[1] = 1
    memo[2] = 1

    for i in range(3, n + 1):
        memo[i] = memo[i - 1] + memo[i - 2]

    return memo[n]

print(fib(6))

এই পদ্ধতিতে অনেক দ্রুত ফিবোনাচি সংখ্যা বের করা যাবে। কম্পিউটার হ্যাং করবে না!

রিকার্শন ও ডাইনামিক প্রোগ্রামিং

যে সব অ্যালগরিদম গুলো রিকার্শন ব্যবহার করে সমাধান করা যায়, সেগুলোর মধ্যে কিছু কিছু সমস্যা ডাইনামিক প্রোগ্রামিং ব্যবহার করেও সমাধান করা যাবে। তবে সব রিকার্সিভ সমস্যা ডাইনামিক প্রোগ্রামিং ব্যবহার করে সমাধান করা যাবে না। এর কারণ হচ্ছে ডাইনামিক প্রোগ্রামিং দিয়ে ঐ সমস্যা গুলোই সমাধান করা যাবে, যেগুলোর সাব-প্রবলেম গুলোর সমাধানের মধ্যে মিল থাকে। উপরের ফিবোনাচি সিরিজে যেমন সাব-প্রবলেমের সমাধান গুলোর মধ্যে মিল ছিল বলেই আমরা ঐ সমাধান গুলো মেমোয়াইজ করে রাখতে পেরেছি। আবার ধরি মার্জ সর্টের কথা, মার্জ সর্ট কিন্তু ডাইনামিক প্রোগ্রামিং ব্যবহার করে সমাধান করা যাবে না। এর কারণ হচ্ছে সাব-প্রবলেম গুলোর সমাধানের মধ্যে কোন মিল থাকবে না।