লিনিয়ার রিগ্রেশন, গ্র্যাডিয়েন্ট ডিসেন্ট ও পেছনের গণিত

লিনিয়ার রিগ্রেশন

দুই বা তার অধিক ভ্যারিয়েবলের মধ্যে সম্পর্ক খুঁজে বের করা হচ্ছে রিগ্রেশন। মেশিন লার্নিং অথবা স্ট্যাটিসটিক্সে এই সম্পর্ক ব্যবহার করে ফিউচার ভ্যালুর আউটকাম প্রিডিক্ট করা যায়। ভ্যারিয়েবল গুলোর মধ্যে সম্পর্ক সরল রেখা দিয়ে প্রকাশ করা হচ্ছে লিনিয়ার রিগ্রেশন। এখানে অ্যালগরিদম ভ্যারিয়েবল গুলোর মধ্যে একটা লাইন খুঁজে বের করে। যে লাইন সবচেয়ে নির্ভুল ভাবে ভ্যারিয়েবল গুলোর মধ্যে সম্পর্ক বের করা হচ্ছে অ্যালগরিদমের মূল লক্ষ্য।যার ফলে একটা ভ্যারিয়েবলের ভ্যালু দিয়ে অন্য আরেকটা ভ্যারিয়েবলের ভ্যালু প্রিডিক্ট করা যায়।

যে ভ্যারিয়েবলের ভ্যালু আমরা প্রিডিক্ট করব, তা হচ্ছে ডিপেন্ডেন্ট ভ্যারিয়েবল। আর প্রিডিক্ট করার জন্য যে ভ্যারিয়েবলের ভ্যালু দিব, তা হচ্ছে ইন্ডিপেন্ডেন্ট ভ্যারিয়েবল।

দুইটা ভ্যারিয়েবলের মডেলকে বলা হয় সিম্পল লিনিয়ার রিগ্রেশন মডেল। দুইয়ের অধিক ভ্যারিয়েবল যদি জড়িত থাকে, তাহলে তাকে বলে মাল্টি লিনিয়ার রিগ্রেশন মডেল। বুঝার সুবিধার্থে আমরা শুধু মাত্র দুইটা ভ্যারিয়েবল নিয়ে চিন্তা করতে পারি। একটা ডিপেন্ডেন্ট ভ্যারিয়েবল, আরেকটা ইন্ডিপেন্ডেন্ট ভ্যারিয়েবল।

ডেটা

ডেটা হিসেবে আমরা ঢাকার বাসা ভাড়ার উদাহরণ নিতে পারি। একটা বাসা যত বড় হয়, সাধারণত ঐ বাসার ভাড়া তত বেশি থাকে। আবার লোকেশন, বাসা কত পুরাতন, ইন্টারিয়র এসবও গুরুত্বপূর্ণ প্যারামিটার। সহজ রাখার জন্য আমরা এখন শুধু মাত্র স্কয়ার ফিট এবং ভাড়াটাই দেখব। নিচের ডেটা গুলো দেখিঃ

Square feet	Rent
500	10000
600	12500
700	13000
800	13500
1000	14000
1200	19000
1400	21000
1500	25000
1800	28000

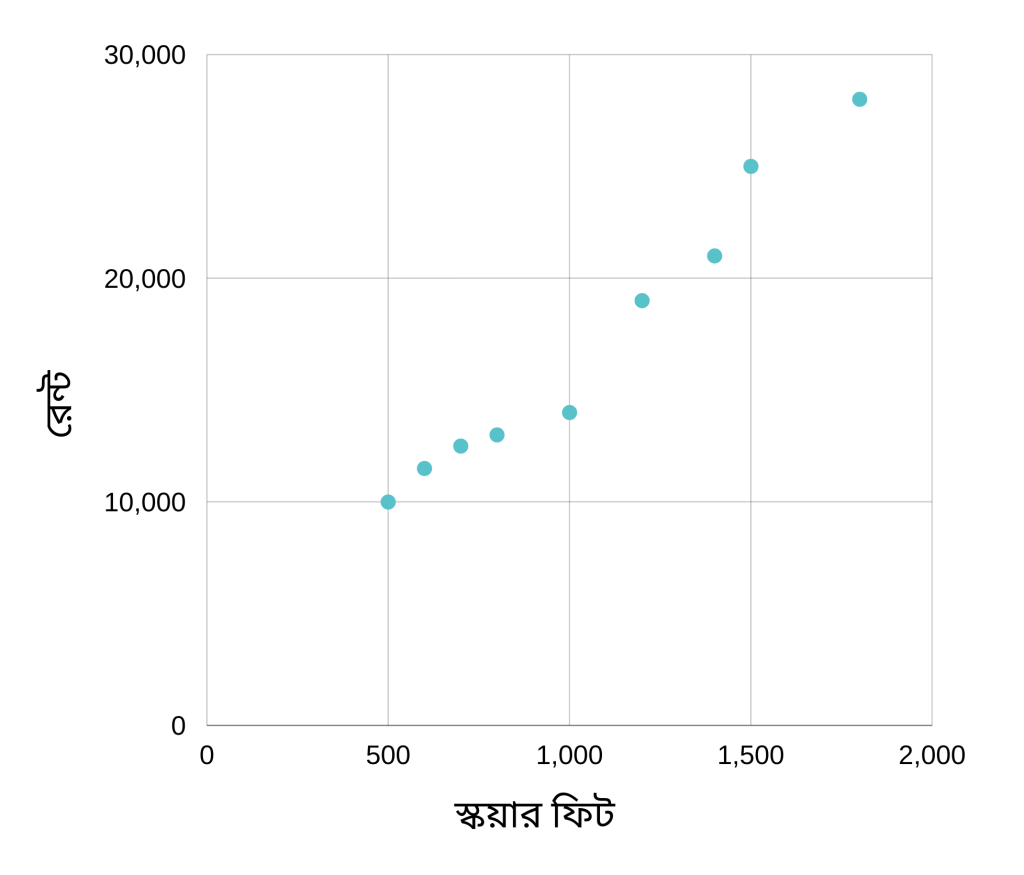
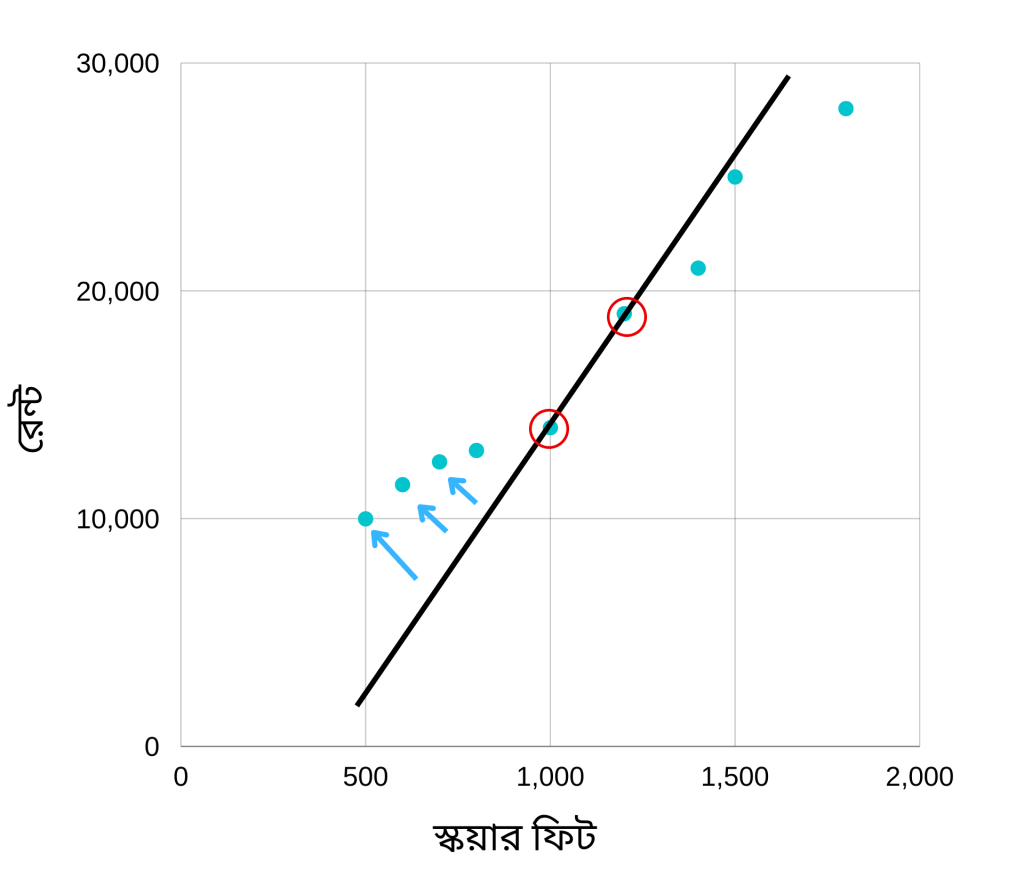
এই ডেটা গুলোর উপর ভিত্তি করে আমরা এমন একটা মডেল তৈরি করব, যেখানে কোন একটা বাসার সাইজ দিলে ঐ বাসার ভাড়া কত হতে পারে, আমাদের তা রিটার্ণ করবে। তো এই মডেলটা তৈরি করার আগে ডেটা গুলো পরীক্ষা করে দেখব। ডেটা পরীক্ষা করার সবচেয়ে ভালো মাধ্যম হচ্ছে ডেটা ভিজুয়ালাইজ করা। অনেক ভাবেই ডেটা ভিজ্যুয়ালাইজ করা যায়। আমাদের ডেটা যেমন সিম্পল, আমরা তেমন সিম্পল ভিজ্যুয়ালাইজার স্ক্যাটার প্লট করে দেখতে পারি।

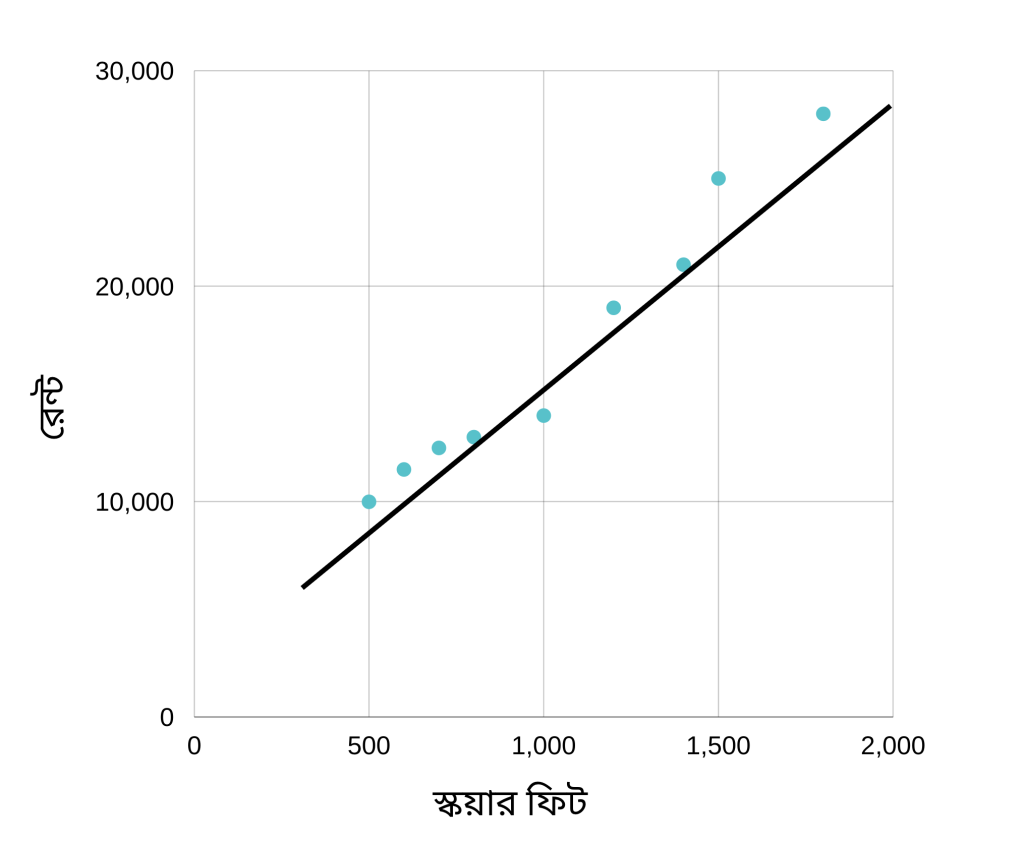
উপেরর স্ক্যাটার প্লট এনালাইসিস করলে আমরা দেখব যে বাসার সাইজ যত বড় হবে, তার ভাড়া তত বেশি হবে। এই ডেটা থেকে আমরা আরেকটা বিষয়ও দেখতে পাচ্ছি যে বাসা সাইজ এবং ভাড়ার মধ্যে একটা লিনিয়ার সম্পর্ক রয়েছে। মানে আমরা একটা লাইন আঁকতে পারি এভাবেঃ

যদিও লাইনটি প্লটের সব গুলো পয়েন্টের মধ্য দিয়ে যায় নি তবে এটা থেকে আমরা বুঝতে পারি যে বাসা সাইজ এবং ভাড়ার সম্পর্কটা একটা লিনিয়ার সম্পর্ক। আর যে কোন লিনিয়ার ফাংশনের সমীকরণ হচ্ছেঃ

Y = mX + b

এখানে

• Y = বাসা বাড়া
• X = বাসার সাইজ
• m = লাইনের স্লপ বা ঢাল। আরো সহজ ভাবে বললে লাইনটা কতটুকু খাড়া, তা।
• b = লাইনটি y কর্ডিনেটের কোন বিন্দুতে মিলিত হয়েছে তা। y ইন্টারসেফট ও বলা হয় একে।।

মেশিন লার্নিং এর ক্ষেত্রে Y কে বা যা প্রিডিকশন করতে হবে, তাকে বলে লেভেল। X বা ইনপুটকে বলা হয় ফিচার। এবং b, m কে বলা হয় ওয়েট।

এখন প্রদত্ত ডেটা থেকে লেভেল গুলো নিয়ে যদি একটা রিগ্রেশন লাইন লাইন তৈরি করি, তাহলে আমরা নতুন ইনপুট ফিচারের জন্য ভ্যালু প্রিডিক্ট করতে পারব। কমপ্লিকেটেড বিষয় গুলো সম্পর্কে জানার আগে যতটুকু শিখেছি, তা দিয়েই আমরা একটা সিম্পল লিনিয়ার রিগ্রেশনের কোড লিখে ফেলতে পারি। আর এই রিগ্রেশন লাইন বের করার জন্য প্রদত্ত ডেটা পয়েন্ট গুলোর এভারেজ নিয়ে রিগ্রেশন লাইন বের করব।

import numpy as np

# sft as X, rent as y 
X = np.array([500, 600, 700, 800, 1000, 1200, 1400, 1500, 1800])
Y = np.array([10000, 12500, 13000, 13500, 14000, 19000, 21000, 25000, 28000])


# Calculate the slope and intercept of the regression line
n = len(X)
x_mean = np.mean(X)
y_mean = np.mean(Y)
numerator = np.sum((X - x_mean) * (Y - y_mean))
denominator = np.sum((X - x_mean) ** 2)
slope = numerator / denominator
intercept = y_mean - slope * x_mean

# Print the slope and intercept of the regression line
print('Slope:', slope)
print('Intercept:', intercept)

# Predict the rent for a new sft value
new_X = 1900 
new_y = slope * new_X + intercept
print('Predicted value of y:', new_y)

এখানে Y = mX + b এই সমীকরণের m হচ্ছে স্লপ এবং b হচ্ছে ইন্টারসেপ্ট। এই দুইটা ভ্যালু বের করলেই আমরা দেখতে পাচ্ছি যে নতুন যে কোন ইনপুটের আউটপুট প্রিডিক্ট করতে পারছি। তাই এই দুইটা ভ্যালু আমরা নিচের কোড দিয়ে ক্যালকুলেট করে নিয়েছিঃ

slope = numerator / denominator
intercept = y_mean - slope * x_mean

উপরের কোড রান করলে নিচের মত করে আউটপুট পাবোঃ

Slope: 13.626907073509011
Intercept: 2949.3758668515966
Predicted value of y: 28840.499306518715

উপরের কোডে new_X এর ভ্যালু পরিবর্তন করে অন্য আরেকটা ভ্যালু দিয়ে তার আউটপুট প্রিডিক্ট করে দেখতে পারি।

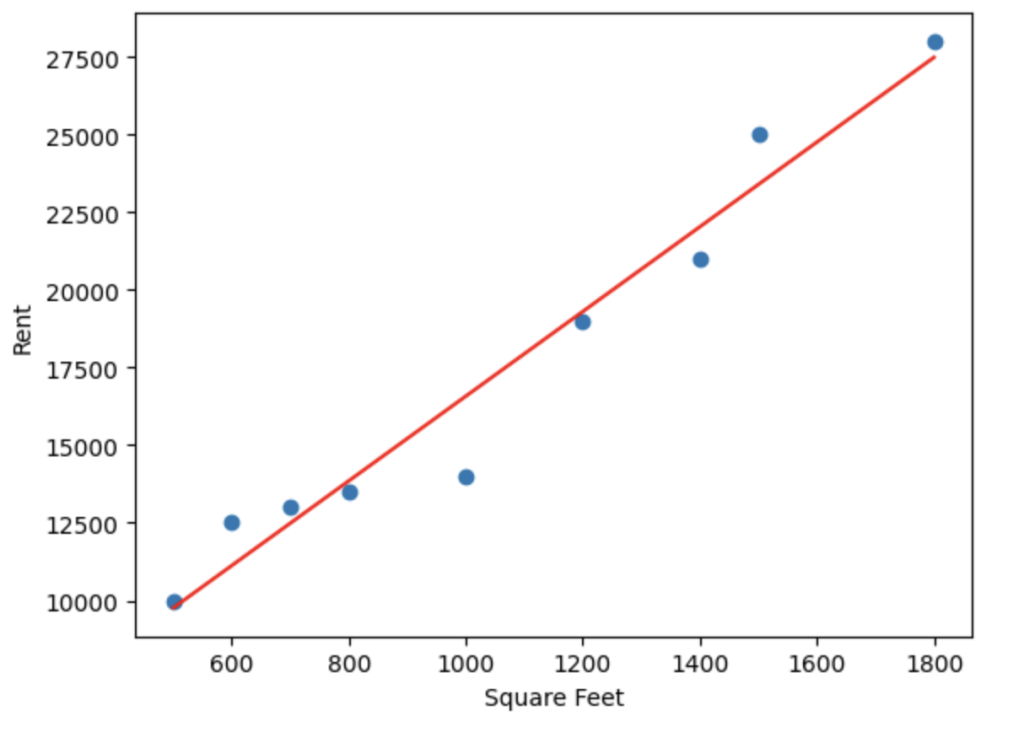
আমরা চাইলে গ্র্যাডিয়েন্ট লাইন এভাবে প্লট করে দেখতে পারিঃ

import matplotlib.pyplot as plt
plt.scatter(X, Y)
plt.plot(X, slope * X + intercept, color='red')

আউটপুট পাবোঃ

আগের কোডের সাথে এই কোড গুলো যোগ করলে পাবোঃ

import numpy as np
import matplotlib.pyplot as plt

# sft as X, rent as y 
X = np.array([500, 600, 700, 800, 1000, 1200, 1400, 1500, 1800])
Y = np.array([10000, 12500, 13000, 13500, 14000, 19000, 21000, 25000, 28000])


# Calculate the slope and intercept of the regression line
n = len(X)
x_mean = np.mean(X)
y_mean = np.mean(Y)
numerator = np.sum((X - x_mean) * (Y - y_mean))
denominator = np.sum((X - x_mean) ** 2)
slope = numerator / denominator
intercept = y_mean - slope * x_mean

# Print the slope and intercept of the regression line
print('Slope:', slope)
print('Intercept:', intercept)

# Predict the rent for a new sft value
new_X = 1900 
new_y = slope * new_X + intercept
print('Predicted value of y:', new_y)

# Plot the data points and the regression line
plt.scatter(X, Y)
plt.xlabel('Square Feet')
plt.ylabel('Rent')
plt.plot(X, slope * X + intercept, color='red')

উপরের প্রোগ্রাম আউটপুট দিবেঃ

Slope: 13.626907073509011
Intercept: 2949.3758668515966
Predicted value of y: 28840.499306518715

এবং নিচের প্লট দেখাবেঃ

বেশির ভাগ ডেটার ক্ষেত্রে এমন এভারেজ নিয়ে রিগ্রেশন লাইন জেনারেট করলে খুব একটা একুরেট প্রিডিকশন দিতে পারবে না। আমরা যখন লিনিয়ার রিগ্রেশন দিয়ে কোন সমস্যা সমাধান করব, তখন মূলত আমরা যে স্যাম্পল ডেটা দিব, ঐ ডেটা থেকে রিগ্রেশন লাইনের এই সমীকরণটি বের করার চেষ্টা করবে। যেটাকে বলা হয় মডেল ট্রেইনিং।

ট্রেইনিং

মডেল ট্রেইনিং হচ্ছে প্রদত্ত ডেটা থেকে ওয়েট এবং বায়াসের ভ্যালু নির্ধারণ। একটা মডেল ট্রেইন করার সময় লক্ষ্য থাকে লস মিনিমাইজ করা। উপরের উদাহরণ যদি চিন্তা করি আমাদের লক্ষ্য হচ্ছে এমন একটা লাইন খুঁজে বের করা, যেটা ডেটা গুলোকে সঠিক ভাবে রিপ্রেজেন্ট করে। Y = mX + b ইকুয়েশনের ক্ষেত্রে ওয়েট হচ্ছে m বায়াস হচ্ছে b।

ইরর বা লস

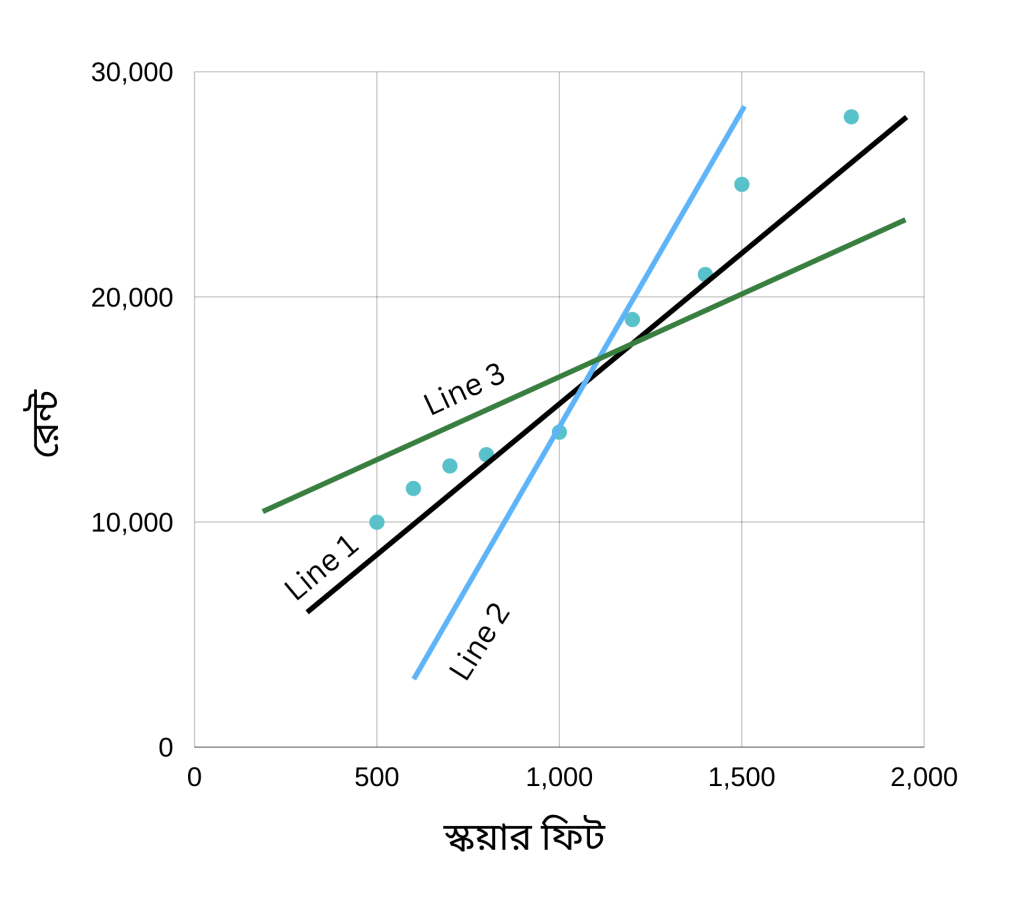
লস হচ্ছে ভুল প্রিডিকশনের পরিমাণ। মডেল যদি সঠিক ভাবে প্রিডিক্ট করতে পারে, তাহলে লস হচ্ছে শূন্য। আর সঠিক ভাবে যদি প্রিডিক্ট করতে না পারে, তাহলে লস একটা পজেটিভ সংখ্যা। ধরে নিচ্ছি আমাদের মডেল তিনটে রিগ্রেশন লাইন তৈরি করেছে। নিচের প্লট দেখিঃ

এখানে লক্ষ্য করি, মডেল তিনটে প্রিডিকশন করেছে। প্লট থেকে দেখতে পাচ্ছি যে এর মধ্যে Line 1 ভুল কম করেছে। বাকি দুইটা লাইন ভুল বেশি করেছে।

ইরর ক্যালকুলেশনঃ
মডেল যে লাইনটি প্রিডিক্ট করে, তা থেকে সত্যিকারের ভ্যালু কত দূর, তাই হচ্ছে লস।

উপরের প্লটটি দেখি। এখানে দুইটা ভ্যালুর জন্য মডেল সঠিক প্রিডিকশন দিতে পেরেছে। এর মানে হচ্ছে ঐ দুইটা ভ্যালুর জন্য ইরর হচ্ছে শূন্য। বাকি গুলোর জন্য ইরর হচ্ছে লাইন থেকে সত্যিকারের ভ্যালু কত দূর, তা। এটাকে যদি সমীকরণ আকারে লিখি তাহলে এভাবে লিখতে পারিঃ

ইরর = মূল ভ্যালু – প্রিডিকশন।

যেমন মূল ভ্যালু (লেভেল) হচ্ছে 18000 কিন্তু প্রিডিক্ট করেছে 16000, তাহলে
ইরর = 18000 – 16000 = 2000

আবার মূল ভ্যালু (লেভেল) হচ্ছে 13000 কিন্তু প্রিডিক্ট করেছে 16000। তাহলে
ইরর = 13000 – 16000 = – 3000

মডেলের ইরর যখন ক্যালকুলেট করি, তখন তার পজেটিভ ভ্যালু নিতে হয়। ইরর তো নেগেটিভ হতে পারে না। মানে যে কোন ইররই হচ্ছে মডেলের ব্যর্থতা। তা পজেটিভ হোক বা নেগেটিভ। তো এই জন্য আমাদের ইরর ক্যালকুলেশন করার সময় তাকে পজেটিভ করে নিতে হয়। পজেটিভ করার অনেক গুলো পদ্ধতির মধ্যে একটা হচ্ছে ভ্যালুটাকে বর্গ করা। যাকে বলা স্কয়ার্ড ইরর।

স্কয়ার্ড লস = (মূল ভ্যালু – প্রিডিকশন)²

যাকে সাধারণত এভাবে প্রকাশ করা হয়ঃ

Squared Loss = (Y – Y’)²

Mean Square error (MSE): ডেটা সেটের প্রতিটা উদাহরণের ইরর ক্যালকুলেশন করতে হবে আমাদের। সম্পূর্ণ ডেটা সেটের প্রতিটা উদাহরণের স্কয়ার লসের গড় হচ্ছে এই MSE। যাকে ম্যাথম্যাটিক্যালি এভাবে প্রকাশ করতে পারিঃ

MSE = \frac{1}{N} \sum_{i=0}^n (Y - Y')^2

এখানে:

• N হচ্ছে এই D ডেটাসেটে টোটাল উদাহরণ।
• X হচ্ছে ফিচার বা বাসার সাইজ।
• Y হচ্ছে লেভেল বা বাসা ভাড়া।
• Y’ কে বলতে পারি আমাদের মডেলের আউটপুট। যেখানে X ইনপুট হিসেবে দিলে আউটপুট Y’ পাওয়া যাবে।

MSE হচ্ছে অনেক গুলো লস ফাংশনের মধ্যে একটা। এটা ছাড়াও আরো লস ফাংশন রয়েছে। তবে MSE সবচেয়ে বেশি ব্যবহৃত একটা লস ফাংশন।

এখন প্রশ্ন করতে পারেন কেন আমরা ইররের পার্থক্যের বর্গ করে নিচ্ছি, কেন ইররের পরম মান নিচ্ছি না। পরম মান নিলেও তো তা পজেটিভ থাকে। এর কারণ হচ্ছে ইররের পার্থক্যের বর্গ থেকে রিগ্রেশন লাইনের ডিরেভেটিভ বের করা সহজ হয়। আমাদের মূল লক্ষ্য হচ্ছে কষ্ট ফাংশনের প্রথম ডিরেভেটিভ বের করা। তো কোন অ্যাবসলিউট ভ্যালুর ডিরেভেটিব বের করা থেকে স্কয়ার ভ্যালুর ডিরেভেটিব বের করা সহজ।

লস তো ক্যালকুলেট করলাম MSE এর মাধ্যমে। এরপরবর্তী কাজ হচ্ছে লস কমানো। লস কমানোরও অনেক গুলো পদ্ধতি রয়েছে। আমরা শিখব গ্র্যাডিয়েন্ট ডিসেন্ট।

কষ্ট ফাংশন মিনিমাইজ করা

শুধু লিনিয়ার রিগ্রেশন না, যে কোন মেশিন লার্নিং অ্যালগরিদমের লক্ষ্যই হচ্ছে কষ্ট ফাংশন মিনিমাইজ করা। কারণ প্রিডিক্টেড ভ্যালু এবং প্রকৃত ভ্যালুর মধ্যে পার্থক্য যত কম হবে, অ্যালগরিদম তত নির্ভুল প্রিডিক্ট করতে পারবে।

Y = mX + b

উপরের সমীকরণের দিকে তাকাই। আমরা ইনপুট দিচ্ছি X। আউটপুট পাচ্ছি Y। এখন অ্যালগরিদম এই দুইটা ভ্যালু পরিবর্তন করে না। অ্যালগরিদম যে ভ্যালু দুইটা পরিবর্তন করে মডেলকে নির্ভুল করার চেষ্টা করে, তা হচ্ছে m এবং b। তো যতটুকু পারা যায় ততটুকু নির্ভুল মডেল পেতে হলে m এবং b এর এমন ভ্যালু পেতে হবে, যেন সবচেয়ে কম ইরর দেয়।

যে কোন ফাংশনকে মিনিমাইজ করা

কষ্ট ফাংশনের সমীকরণের দিকে তাকাইঃ
MSE = \frac{1}{N} \sum_{i=0}^n (Y - Y')^2

যেটাকে Y = X² ফরমে লেখা যায়। যা একটা প্যারাবোলার সমীকরণ। কার্টেসিয়ান কর্ডিনেট সিস্টেমে যা দেখতে নিচের মত দেখাবেঃ

এই ফাংশনকে মিনিমাইজ করা মানে হচ্ছে X এর ঐ ভ্যালুটা খুঁজে বের করা, যা আমাদের Y এর সবচেয়ে ছোট ভ্যালু রিটার্ণ করবে আর যা হচ্ছে 0। আর এই ভ্যালু বের করার জন্য একটা অ্যালগরিদম দরকার, যাকে বলে গ্র্যাডিয়েন্ট ডিসেন্ট।

গ্র্যাডিয়েন্ট ডিসেন্ট

শুধু লিনিয়ার রিগ্রেশনের জন্য না, আরো অনেক গুলো অ্যালগরিদম অপটিমাইজেশনের জন্য গ্র্যাডিয়েন্ট ডিসেন্ট জনপ্রিয় একটা অ্যালগরিদম। এই অ্যালগরিদম ইটারেশনের মাধ্যমে যে কোন ফাংশনের মিনিমা বের করতে সাহায্য করে।

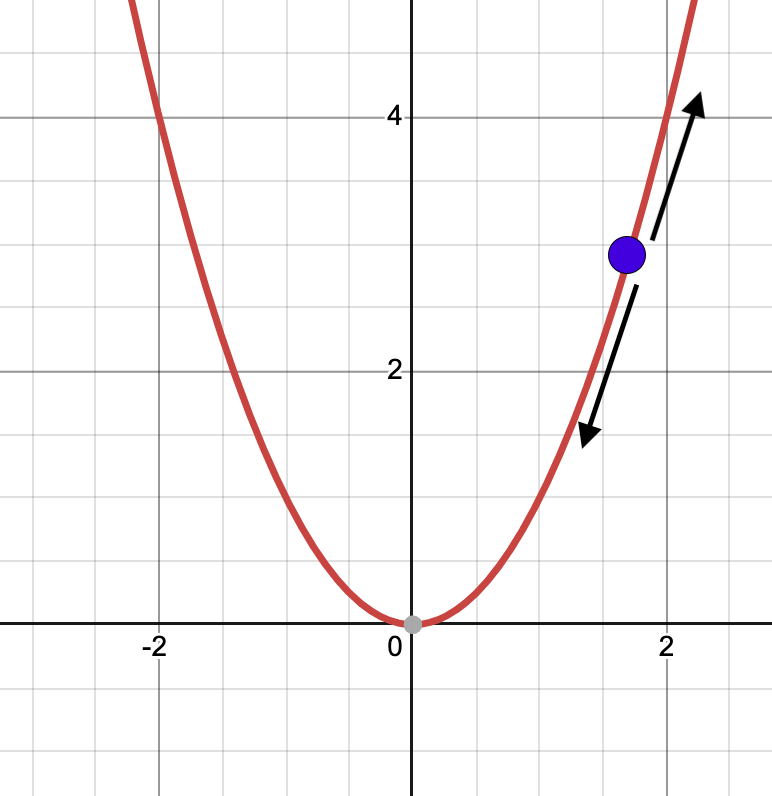
ধরে নিচ্ছি আমরা Y = X² গ্রাফে হাঁটছি। তো আমি এখন রয়েছে গ্রিন ডট পজিশনে। আমার লক্ষ্য হচ্ছে এই ফাংশনের মিনিমাতে পৌঁছানো আর যা হচ্ছে গ্রাফের 0,0 কর্ডিনেটে। আমার পজিশন থেকে তা দেখা যাচ্ছে না। এই মিনিমা বের করার জন্য আমি যে কাজটি করতে পারি, হয় উপরের দিকে যেতে পারি অথবা নিচের দিকে যেতে পারি। এই উপরের দিকে যাওয়া বা নিচের দিকে যার সময় বড় বড় স্টেপে হাঁটতে পারি অথবা ছোট ছোট স্টেপে হাঁটতে পারি।

এখন কোন দিকে হাঁটব, তা বের করতে হবে আমরা কোন পয়েন্টে রয়েছি, সে পয়েন্টের টেনজেন্ট লাইন ব্যবহার করে।

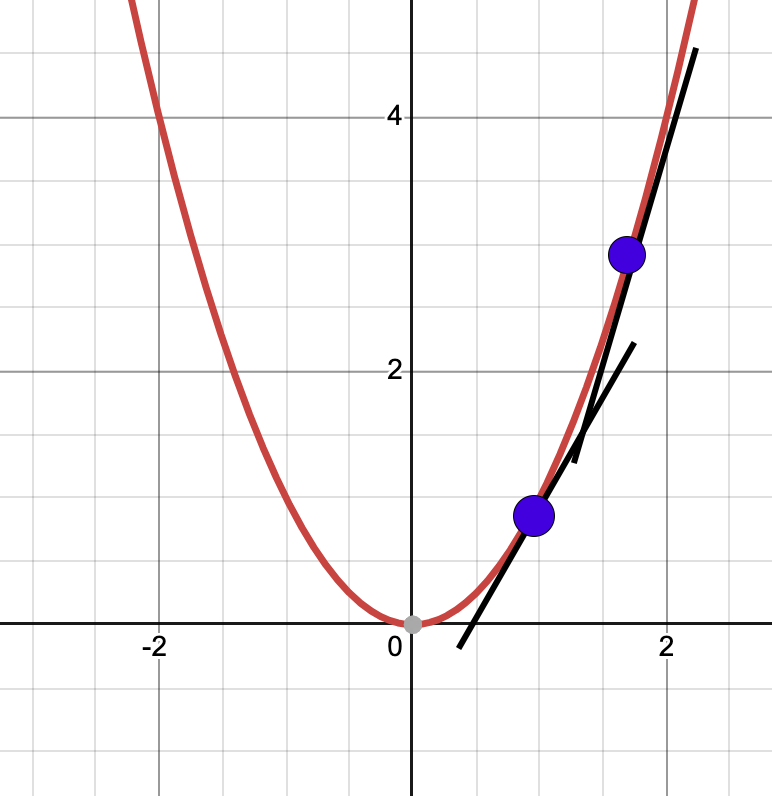
টেনজেন্ট লাইন আঁকার পর বুঝবতে পারব যে আমরা যত উপরের দিকে যাবো ট্যানজেন্ট লাইনের স্লপ তত বেশি হবে মানে তত খাড়া হবে। এর মানে হচ্ছে আমরা মিনিমা থেকে দূরে সরে যাচ্ছি। আবার যদি যত নিচের দিকে যাবো, ট্যানজেন্ট লাইন ঢালু হবে বা স্লোপ তত কম হবে। এর মানে আমরা মিনিমা এর দিকে যাচ্ছি।

উপরের দুইটা পয়েন্টে দুইটা ট্যানজেন্ট লাইন এঁকেছি। এখান থেকে স্পষ্ট বুঝা যাচ্ছে উপরের পয়েন্টের ট্যানজেন্ট লাইনের স্লপ বেশি। নিচেরটার স্লোপ কম।

আমাদের কাজ হচ্ছে স্লপ বের করা। কোন ফাংশনের স্লপ হচ্ছে ঐ ফাংশনের ডেরেভেটিভ। কোন ফাংশনের ডেরিভেটিভ বের করার জন্য ক্যালকুলাস সম্পর্কে জানা দরকার। এই লেখা বুঝার জন্য যতটুকু ক্যালকুলাস জ্ঞান দরকার, তা যোগ করে দিয়েছি।

গ্র্যাডিয়েন্ট ডিসেন্টের স্টার্টিং পয়েন্ট

গ্র্যাডিয়েন্ট ডিসেন্টের প্রথম ধাপ হচ্ছে m এর জন্য একটা স্টার্টিং পয়েন্ট নেওয়া। স্টার্টিং পয়েন্ট খুব একটা রোল প্লে করে না। তো বেশির ভাগ অ্যালগরিদমে m এবং b এর ভ্যালু 0 ধরে নেয়। এরপর গ্র্যাডিয়েন্ট ডিসেন্ট অ্যালগরিদম ঐ স্টার্টিং পয়েন্টের লসের গ্র্যাডিয়েন্ট ক্যালকুলেট করে। গ্র্যাডিয়েন্ট হচ্ছে ঐ পয়েন্টের ডেরিভেটিভ বা স্লপ। এই গ্র্যাডিয়েন্ট একটা ভেক্টর। তাই এর মান এবং দিক রয়েছে। গ্র্যাডিয়েন্টের দিক হচ্ছে খাড়া এর দিকে। তো মিনিমায় পৌঁছানোর জন্য গ্র্যাডিয়েন্ট ডিসেন্ট অ্যালগরিদম নেগেটিভ গ্র্যাডিয়েন্টের দিকে যায়। কত স্টেপ যাবে, তাই হচ্ছে লার্নিং রেট।

লার্নিং রেট

প্রতি ইটারেশনে কতটুকু ধাপ সামনে এগুবে, তাই হচ্ছে লার্নিং রেট। যদি আমরা হেঁটে হেঁটে নামার সাথে তুলনা করি, তাহলে লার্নিং রেট হচ্ছে এক কদমে কতটুকু দূরত্ব যাচ্ছি, তা। যদি বড় বড় কদমে হাঁটি, তাহলে আমরা হয়তো মিনিমাকে রেখে চলে যাবো। আবার যদি ছোট ছোট কদমে হাঁটি, তাহলে মিনিমায় পৌঁছাতে বেশি সময় লাগবে।

দরকারি গণিত – ডেরিভেটিভ

ফাংশনের প্যারামিটার বা ওয়েট গুলো বাড়াবে নাকি কমাবে, তা ডেরিভেটিভ দিয়ে বের করা হয়। কোন ফাংশনের ডেরিভেটিভ ক্যালকুলেট করলে বুঝা যায় ঐ ফাংশনটির মিনিমা কোন দিকে।

গ্র্যাডিয়েন্ট ডিসেন্টের মিনিমা বের করার জন্য ডেরিভেটিভের দুইটা সূত্র জানা লাগবে। একটা হচ্ছে Power Rule আরেকটা হচ্ছে Chain Rule। এই দুইটা সূত্র সম্পর্কে জানলে বিষয় গুলো বুঝতে সুবিধে হবে।

Power Rule:

যেমন একটা ফাংশন হচ্ছেঃ
f(x) = x^n
এর ডেরিভেটিভ হবে:
\frac{d}{dx} x^n = n.x^{n-1}
একটা উদাহরণ দেওয়া যাকঃ
একটা ফাংশনf(x) = x^4 এর ডেরিভেটিভ হবে:
\frac{d}{dx} x^4 = 4x^3
Chain Rule:
একটা ফাংশনের ভেতর যদি আরেকটা ফাংশন থাকে, তাহলে ঐ ধরণের ফাংশনের ডেরিভেটিভ বের করার জন্য চেইন রুল ব্যবহার করা হয়। যদি ভ্যারিয়েবল z ভ্যারিয়েবল y এর উপর নির্ভরশীল হয় এবং ভ্যারিয়েবল y যদি আবার ভ্যারিয়েবল x এর উপর নির্ভশীল হয়, তাহলে চেইন রুলের সূত্র হচ্ছেঃ
\frac{dy} {dz} = \frac{dy}{dx} \frac{dx}{dz}
একটা উদাহরণের সাহায্যে বুঝা যাক। যদি y = x² এবং x = z² হয় , তাহলে z এর সাপেক্ষে y এর ডেরিভেটিভ হবে:
\frac{dy} {dz} = \frac{dy}{dx} \frac{dx}{dz}
এখানেঃ
\frac{dy}{dx} = 2x
এবং
\frac{dx}{d} = 2z
তাহলে
\frac{dy} {dz} = 2x.2z
পার্শিয়াল ডেরিভেটিভঃ
একটা ফাংশনে যদি দুইটা ভ্যারিয়েবল থাকে, তাহলে ঐ ফাংশনের একটা ভ্যারিয়েবলের সাপেক্ষে আরেকটা ভ্যারিয়েবলকে কনস্ট্যান্ট ধরে ডেরিভেটিভ বের করা হচ্ছে পার্শিয়াল ডেরিভেটিভ।

উদাহরণ হিসেবে নিচের ইকুয়েশনটি দেখিঃ
f(x,y) = x^4 + y^6
X এর সাপেক্ষে যদি ফাংশনটির ডেরিভেটিভ বের করি, তাহলে y কে কনস্ট্যান্ট ধরতে হবে। তাহলে x এর সাপেক্ষে এই ফনাশনটির ডেরিভেটিভ হবেঃ

\frac{df} {dx} = 4x^3 + 0
[এখানে পাওয়ার রুল ব্যবহার করা হয়েছে। এছাড়া কোন কনস্ট্যান্টের ডেরিভেটিব হচ্ছে 0 ]

আবার যদি y এর সাপেক্ষে যদি ফাংশনটির ডেরিভেটিভ বের করি, তাহলে x কে কনস্ট্যান্ট ধরতে হবে। তাহলে x এর সাপেক্ষে এই ফনাশনটির ডেরিভেটিভ হবেঃ
\frac{df} {dy} = 0 + 5y^4

ইরর ফাংশনের গাণিতিক রূপ

আগেই যেনেছি Y = mX + b সমীকরণের m এবং b এর ভ্যালু পরিবর্তন করে মডেলকে নির্ভুল করার চেষ্টা করতে হয়। এগুলোকে বলে প্যারামিটার। তো ট্রেইনিং প্রসেসে প্রতিটা ইটারেশনে m এবং b এর ভ্যালু অল্প অল্প করে পরিবর্তন করতে হয়। ধরে নেই ঐ ছোট পরিবর্তন হচ্ছে δ। প্রতি ইটারেশনে প্যারামিটারের মান আপডেট হবে এভাবেঃ

m = m – δm
b = b – δb

m এবং b এর ঐ ভ্যালুটা বের করতে হবে যেখানে কষ্ট ফাংশনের ভ্যালু মিনিমাম হয়।

ইরর ফাংশনের দিকে তাকাইঃ
MSE = \frac{1}{N} \sum_{i=0}^n (Y - Y')^2
ইরর ফাংশনকে E দিয়ে প্রকাশ করি যেখানে E হচ্ছে m এবং b এর একটা ফাংশনঃ
E_{m,b} = \frac{1}{N} \sum_{i=0}^n (Y - Y')^2
এখানে Y – Y’ হচ্ছে এরর।

গ্র্যাডিয়েন্ট ডিসেন্ট ক্যালকুলেট করা

ইরর ফাংশন হচ্ছেঃ
E_{m,b} = \frac{1}{N} \sum_{i=0}^n (Y - Y')^2
এখান m এবং b এর সাপেক্ষে আলাদা আলাদা ভাবে কষ্ট ফাংশনের ডেরিভেটিভ ক্যালকুলেট করব। প্রথমে দেখি m এর সাপেক্ষে কষ্ট ফাংশনের ডেরিভেটিভঃ

\frac{dE} {dm} = \frac{1}{N} \sum_{i=0}^n 2. (Y - Y') . \frac{d} {dm} (Y - Y')

[স্লপের গ্র্যাডিয়েন্ট δm]

এখানে
\frac{d} {dm} (Y - Y' ) = \frac{d} {dm} (Y - (mX + b)) = -X
[কারণ এখানে Y’, X এবং b হচ্ছে কনস্ট্যান্ট। আর কনস্ট্যান্টের ডেরিভেটিভ 0 ]

তাহলে স্লপের গ্র্যাডিয়েন্ট ইকুয়েশন দাঁড়ায়ঃ

\frac{dE} {dm} = \frac{-2}{N} \sum_{i=0}^n (Y - Y') . X

পাইথনে যদি লিখি, এভাবে লিখতে পারিঃ

(-2/len(X)) * np.sum(X * (Y - y_pred))

এবং b এর সাপেক্ষে কষ্ট ফাংশনের ডেরিভেটিভঃ

\frac{dE} {db} = \frac{1}{N} \sum_{i=0}^n 2. (Y - Y') . \frac{d} {db} (Y - Y')

[ইন্টারসেফটের গ্র্যাডিয়েন্ট δb]

এখানে
\frac{d} {db} (Y - Y' ) = \frac{d} {db} ( Y - ( mX + b)) = -1
[এখানে Y’, X এবং b হচ্ছে কনস্ট্যান্ট]

তাহলে ইন্টারসেফটের গ্র্যাডিয়েন্ট ইকুয়েশন দাঁড়ায়ঃ

\frac{dE} {db} = \frac{-2}{N} \sum_{i=0}^n (Y - Y')

পাইথনে যদি এটাকে লিখি, এভাবে লিখতে পারিঃ

(-2/len(X)) * np.sum(Y - y_pred) 

এর আগে লার্নিং রেট সম্পর্কে জেনেছি। প্রতি স্টেপে কত দূর এগুবে, তা ঠিক করে দেয় এই লার্নিং রেট। এখন আমরা স্লপ এবং ইন্টারসেফটের যে গ্র্যাডিয়েন্ট বের করেছি, তাকে লার্নিং রেট দিয়ে গুন করে পূর্বের স্লপ এবং ইন্টারসেফট থেকে বিয়োগ করলেই নতুন স্লপ এবং ইন্টারসেফট পেয়ে যাবো। ইকুয়েশন আকারেঃ

নতুন স্লপ (m) = পূর্ববর্তী স্লপ – (লার্নিং রেট * স্লপ গ্র্যাডিয়েন্ট)

নতুন ইন্টারসেফট (b) = পূর্ববর্তী ইন্টারসেফট – (লার্নিং রেট * ইন্টারসেফট গ্র্যাডিয়েন্ট)

বা:
m = m – learning_rate * δm
b = b – learning_rate * δb

লেখাটির শুরুতে যে রিগ্রেশন লাইনটি বের করেছি, তা বের করেছি ডেটা পয়েন্টের এভারেজ ভ্যালু নিয়ে। এখন আমরা গ্র্যাডিয়েন্ট ডিসেন্ট ব্যবহার রিগ্রেশন লাইন ব্যবহার করব। এখন উপরে আমরা গ্র্যাডিয়েন্ট বের করার যে সমীকরণ বের করেছি, সেগুলো ব্যবহার করে রিগ্রেশন লাইন বের করার চেষ্টা করব।

import numpy as np
import matplotlib.pyplot as plt

# Generate sample data
X = np.array([1, 2, 3, 4, 5, 6])
Y = np.array([33.8, 35.6, 37.4, 39.2, 41, 42.8])


# Initialize the slope and intercept
slope = 0
intercept = 0

# Set the learning rate and number of epoch
learning_rate = 0.01
epochs = 1000

# Perform gradient descent
for i in range(epochs):
    # Calculate the predicted values
    y_pred = slope * X + intercept
    
    # Calculate the gradients
    slope_gradient = (-2/len(X)) * np.sum(X * (Y - y_pred))
    intercept_gradient = (-2/len(X)) * np.sum(Y - y_pred)
    
    # Update the parameters
    slope -= learning_rate * slope_gradient
    intercept -= learning_rate * intercept_gradient

# Pridict for new value 
new_X = 7
new_y = slope * new_X + intercept
print('Predicted value of y:', new_y)

# Plot the data points and the regression line
plt.scatter(X, Y)
plt.plot(X, slope*X + intercept, color='red')
plt.xlabel('Celcius')
plt.ylabel('Farenheit')
plt.show()

উপরের প্রোগ্রাম রান করলে আউটপুট পাবোঃ

Predicted value of y: 45.09126643327592

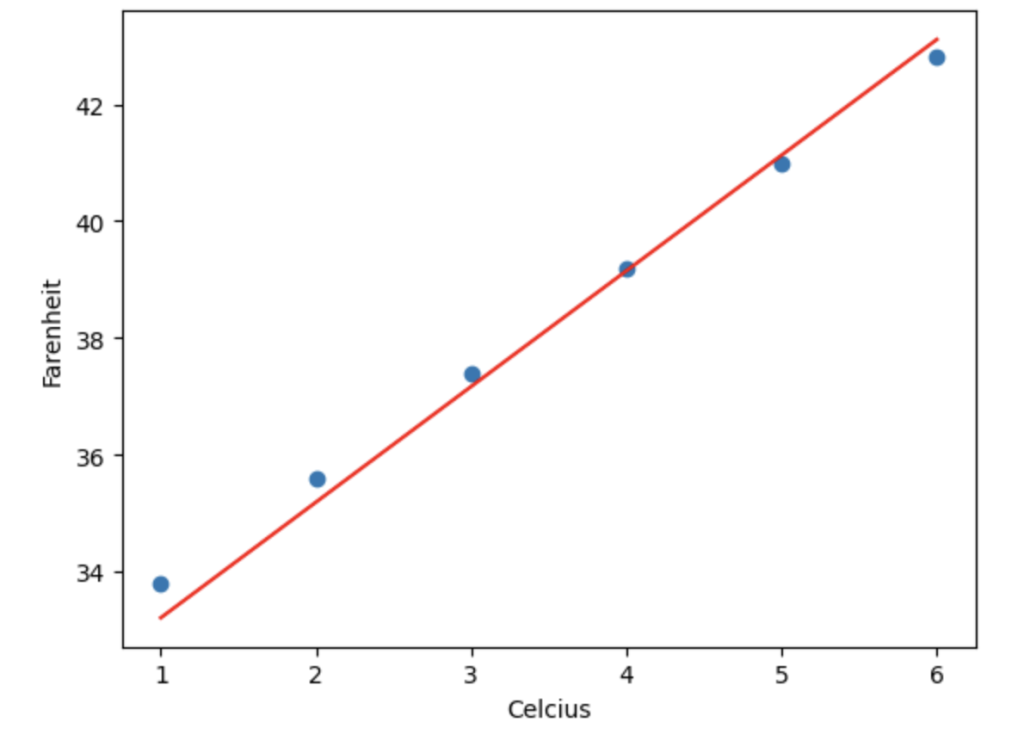
এবং নিচের প্লট দেখাবেঃ

এখানে আমরা শুরুতে স্লপ এবং ইন্টারসেফটকে 0 ধরে নিয়েছি। এরপর গ্র্যাডিয়েন্ট ডিসেন্টের জন্য কতবার ইটারেশন করবে, তা সেট করে দিয়েছি। উপরের প্রোগ্রামে ইটারেশন সেট করেছি 1000 এবং লার্নিং রেট সেট করেছি 0.01।

এখানে আমরা লস ফাংশন হিসেবে ব্যবহার করেছি Mean Sqared Error। আর এই MSE এর পার্শিয়াল ডেরিভেটিভের মাধ্যমে গ্র্যাডিয়েন্ট লাইনের স্লপ এবং ইন্টারসেফটের গ্র্যাডিয়েন্ট বের করেছি। এরপর সূত্র অনুযায়ী নতুন স্লপ এবং ইন্টারসেফট বের করেছি। যা দিয়ে নতুন যে কোন ইনপুটের জন্য আউটপুট প্রিডিক্ট করেছি।
উপরের কোড গুলো গুগল কোল্যাবে পাওয়া যাবে। মেশিন লার্নিং নিয়ে অন্যান্যয় লেখা গুলো পাওয়া যাবে এই পেইজে।