গ্রাফঃ
আমাদের এমন কিছু ডেটা থাকতে পারে, যেগুলোকে ক্রমানুসারে রাখা যায় না। কিন্তু একটা ডেটা আরেকটা ডেটার সাথে র্যানন্ডমলি কানেক্টেড। এমন ডেটা স্টোর করার জন্য দরকার পড়ে গ্রাফ ডেটা স্ট্রাকচারের। যেমন ম্যাপের কথা ধরতে পারি। ম্যাপের প্রতিটা শহর একটা আরেকটার সাথে কানেক্টেড থাকে। এই ম্যাপ ডেটার মত ডেটা গুলো কম্পিউটারে স্টোর করার জন্য যে ডেটা স্ট্রাকচার লাগে, তাই হচ্ছে গ্রাফ।
গ্রাফ হচ্ছে কত গুলো নোড (Node) বা ভার্টেক্স(vertice) এবং এজের (Edge) সমষ্টি। নিচে একটি গ্রাফের ছবি দেওয়া হলোঃ
এ গ্রাফে পাঁচটি নোড বা ভার্টেক্স রয়েছে। নোড গুলো হচ্ছেঃ A, B, C, D এবং E। আর উপরের গ্রাফে এজ রয়েছে ৭টি। গ্রাফে নোড গুলোর সংযোগ কারী রেখা হচ্ছে এজ।
গ্রাফকে নিচের মত করে ভাগ করা যায় :
- Directed, weighted edges
- Directed, unweighted edges
- Undirected, weighted edges
- Undirected, unweighted edges
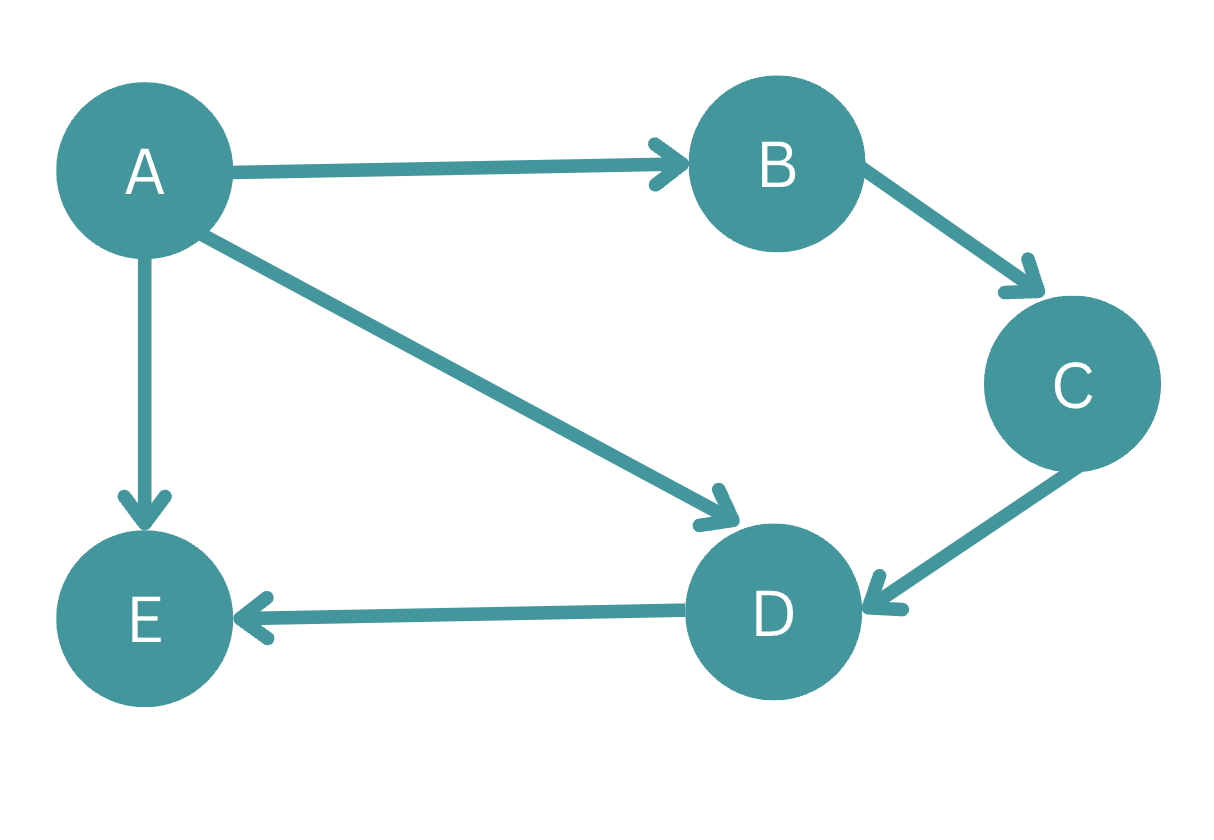
ডিরেক্টেড গ্রাফঃ গ্রাফের এজ গুলোর ডিরেকশন যদি বলা থাকে, তাহলে তাকে ডিরেক্টেড গ্রাফ বলে। নিচের গ্রাফটি একটি ডিরেক্টেড গ্রাফ:
আনডিরেক্টেড গ্রাফঃ গ্রাফের এজ গুলোতে যদি কোন ডিরেকশন না থাকে, সে গুলো হচ্ছে আনডিরেক্টেড গ্রাফ। আনডিরেক্টেড গ্রাপ দ্বিমুখী বা Bidirectional গ্রাফ নামেও পরিচিত।
ওয়েটেড গ্রাফঃ একটা নোড থেকে আরেকটা নোডে যেতে কস্ট উল্লেখ থাকলে সে গ্রাফকে ওয়েটেড গ্রাফ বলে। ওয়েটেড গ্রাফ ডিরেক্টেড এবং আনডিরেক্টেড, দুই ধরনেরই হতে পারে। নিচে একটি ওয়েটেড ডিরেক্টেড গ্রাফের ছবি দেওয়া হলোঃ

আনওয়েটেড গ্রাফঃ একটা নোড থেকে আরেকটা নোডের কস্ট উল্যেখ না থাকলে যে গ্রাফকে আনওয়েটেড গ্রাফ বলে।
অ্যাডজেসেন্ট ভার্টেক্স: একটা ভার্টেক্স যদি আরেকটা ভার্টেক্সের সাথে এজ দ্বারা কানেক্টেড থাকে তাহলে বলা হয় একটা আরেকটার অ্যাডসেসেন্ট ভার্টেক্স।
যেমন উপরের গ্রাফে A কানেক্টেড আছে B এবং E এর সাথে। তাহলে B এবং E হচ্ছে A এর অ্যাডজেসেন্ট ভার্টেক্স। একটা ভার্টেক্সের একের অধিক অ্যাডজেসেন্ট ভার্টেক্স থাকতে পারে। যেমন উপরের গ্রাফে B এর অনেক গুলো অ্যাডজেসেন্ট ভার্টেক্স রয়েছে, সেগুলো হচ্ছেঃ A, C, D এবং E।
গ্রাফ রিপ্রেজেন্টেশনঃ
গ্রাফ দিয়ে অনেক ধরনের সমস্যা সমাধান করা যায়। সমস্যা গুলো সমাধান করার জন্য আমাদের গ্রাফটি কম্পিউটাকে বুঝাতে হবে। কম্পিউটারকে একটা গ্রাফের ছবি দিলে সে বুঝবে না। আর বুঝানোকে বলা হয় গ্রাফ রিপ্রেজেন্টেশন। দুইটা প্রধান উপায় হচ্ছেঃ
- অ্যাডজেসেন্সি ম্যাট্রিক্স।
- অ্যাডজেসেন্সি লিস্ট।
অ্যাডজেসেন্সি ম্যাট্রিক্স রিপ্রেজেন্টেশনঃ
একটি 2D অ্যারে দিয়ে অ্যাডজেসেন্সি ম্যাট্রিক্স রিপ্রেজেন্ট করা হয়। অ্যারের সাইজ হচ্ছে V*V। এখানে V মানে গ্রাফের টোটাল ভার্টেক্স সংখ্যা।
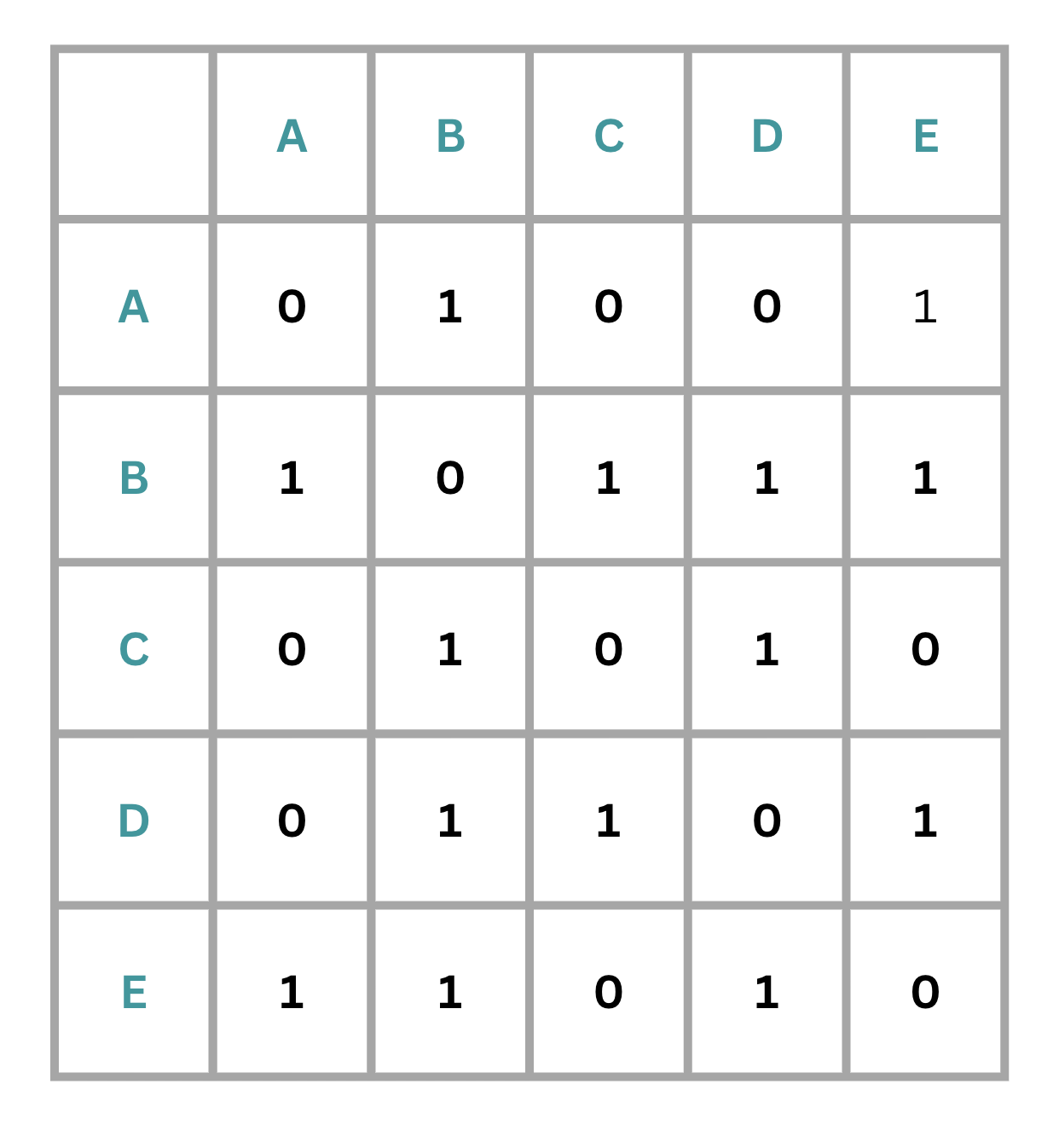
যেমন উপরের গ্রাফে রয়েছে ৫টি ভার্টেক্স। তাহলে আমাদের অ্যারের সাইজ হবে 5*5। কম্পিউটারে সাধানত ইনডেক্স শূণ্য থেকে শুরু হয়। ধরে নিচ্ছিল অ্যারে এর নাম adj, তাহলে অ্যারেটি হবে adj[4][4]। উপরের গ্রাফটির অ্যাডজেসেন্সি ম্যাট্রিক্স রূপ হবে নিচের মত করেঃ
একটা ভার্টেক্সের সাথে যদি একটা ভার্টেক্স কানেকটেড থাকে, তাহলে ঐ অ্যারের ঐ ঘরে একটা 1 বসবে। আর যদি কানেকটেড না থাকে, তাহলে বসবে 0।
উপরের গ্রাফে দেখি A এবং B কানেক্টেড, তাই adj[A][B] = 1 বসেছে। A এবং B কানেক্টেড যে কথা, B এবং A কানেক্টেড ও একই কথা। তাই adj[B][A] তেও 1 বসেছে। এভাবে বাকি গুলো পূরণ করে নিব।
পাইথনে 2D অ্যারে বা ম্যাট্রিক্স রিপজেন্টেশন করা যায় একটা লিস্টের ভেতর আরেকটা লিস্ট ব্যবহার করে। উপরের গ্রাফটি পাইথনে নিচের মত করে রিপ্রেজেন্ট করতে পারিঃ
graph = [ [0, 1, 0, 0, 1], [1, 0, 1, 1, 1], [0, 1, 0, 1, 0], [0, 1, 1, 0, 1], [1, 1, 0, 1, 0] ]
অ্যাডজেসেন্সি লিস্ট রিপ্রেজেন্টেশনঃ
অ্যাডজেসেন্সি ম্যাটিক্স রিপ্রেজেন্টেশন সহজ। ছোট খাটো গ্রাফ রিপ্রেজেন্টেশনের জন্য সুবিধে। সমস্যা হচ্ছে যখন বড় গ্রাফ নিয়ে কাজ করব, তখন এটা তেমন এফিশিয়েন্ট না। প্রোগ্রামারদের সবার আগে যেটা চিন্তা করতে হয়, তা হচ্ছে এফিশিয়েন্সি। যেমন আমরা একটা বিমান কম্পানির জন্য একটা প্রোগ্রাম বানাবো। বিভিন্ন শহরে যাওয়ার সহজ রাস্তা বের করার প্রোগ্রাম লিখতে হবে। তখন আমাদের অনেক গুলো শহর নিয়ে কাজ করতে হবে। যেমন ১০,০০০ টি শহর আছে এবং একটা থেকে আরেকটাতে যেতে ৫০,০০০ পথ রয়েছে। এখন আমরা যদি অ্যাডজেসেন্সি ম্যাটিক্স দিয়ে রিপ্রেজেন্ট করি, তাহলে আমাদের 10,000×10,000 সাইজের একটা অ্যারে ডিক্লেয়ার করতে হবে। যা কম্পিউটারে বিশাল জায়গা দখল করে বসে থাকবে। কিন্তু যার বেশির ভাগই আমাদের দরকার হবে না। আর এই সমস্যা সমাধান করার জন্য আমরা ব্যবহার করব অ্যাডজেসেন্সি লিস্ট।
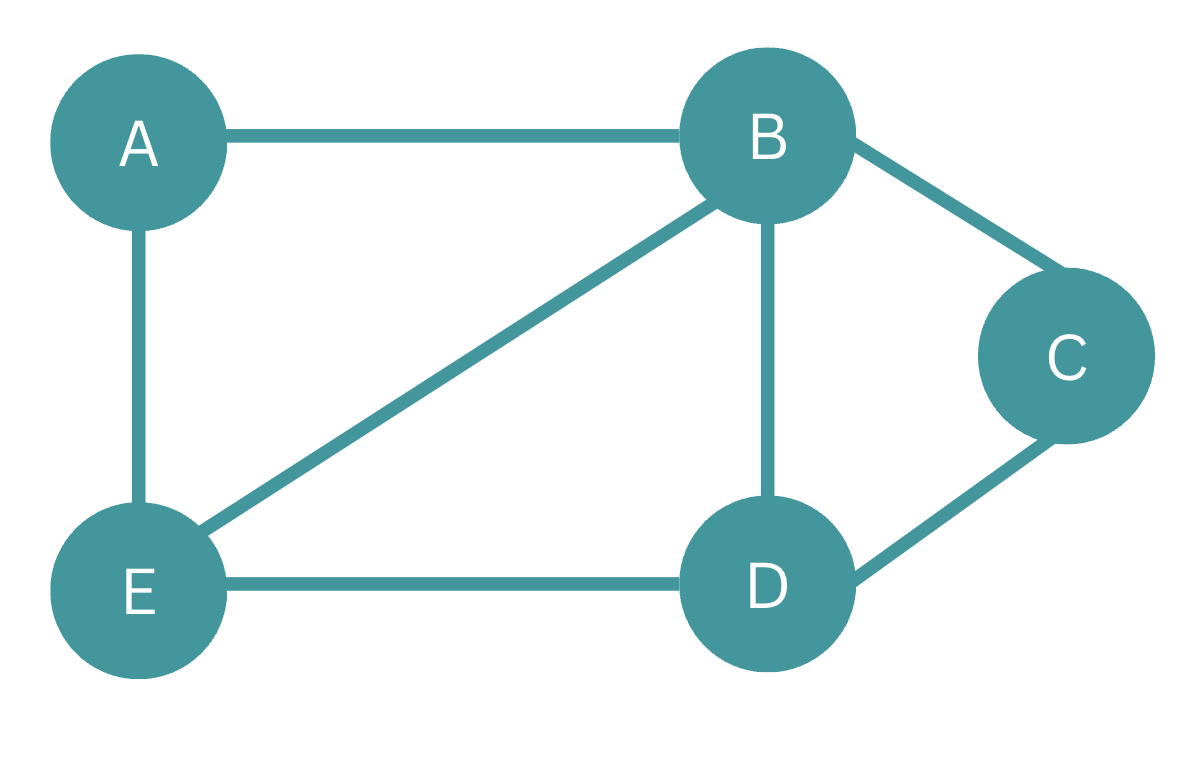
আমাদের উপড়ের গ্রাফটি যদি অ্যাডজেসেন্সি লিস্ট দিয়ে রিপ্রেজেন্ট করি, তাহলে দেখতে নিচের মত হবেঃ
A এর সাথে কানেক্টেড হচ্ছে B & D। যে নোডের সাথে যে নোড কানেক্টেড, আমরা শুধু সে গুলোই লিখেছি। এভাবে বাকি নোড গুলোও।
পাইথনে ডিকশনারি ব্যবহার করে খুব সহজে অ্যাডজেন্সেন্সি লিস্ট রিপ্রেজেন্ট করা যায়ঃ
graph = {
'A': ['B', 'E'],
'B': ['A', 'C', 'D', 'E'],
'C': ['B', 'D'],
'D': ['B', 'C', 'E'],
'E': ['A', 'B', 'D'],
}
for key, val in graph.items():
print(f"{key}-->{val}")
যা রান করলে দেখবঃ
A-->['B', 'E'] B-->['A', 'C', 'D', 'E'] E-->['A', 'B', 'D'] C-->['B', 'D'] D-->['B', 'C', 'E']
উপরে আমরা ম্যানুয়ালি গ্রাফটি তৈরি করেছি। আমরা চাইলে ইউজার থেকে ইনপুট নিয়ে গ্রাফ তৈরি করতে পারিঃ
graph = dict()
def add_edge(node1, node2):
# create an empty list for a key node if it's not exist
if node1 not in graph:
graph[node1] = []
if node2 not in graph:
graph[node2] = []
# append the neighbour node to its corresponding key node
graph[node1].append(node2)
add_edge('A', 'B')
add_edge('A', 'E')
add_edge('B', 'A')
add_edge('B', 'C')
add_edge('B', 'D')
add_edge('B', 'E')
add_edge('C', 'B')
add_edge('C', 'D')
add_edge('D', 'B')
add_edge('D', 'C')
add_edge('D', 'E')
add_edge('E', 'A')
add_edge('E', 'B')
add_edge('E', 'D')
for key, val in graph.items():
print(f"{key}-->{val}")
যা আউটপুট দিবেঃ
A-->['B', 'E'] B-->['A', 'C', 'D', 'E'] E-->['A', 'B', 'D'] C-->['B', 'D'] D-->['B', 'C', 'E']
যদিও উপরে আমরা ইনপুট গুলো কোড করে লিখে দিয়েছি। চাইলে ইউজার থেকে ইনপুট নিয়েও গ্রাফ তৈরি করা যাবে।