একটা সর্টেড লিস্টে টার্গেট আইটেম আছে কিনা, তা খুঁজে বের করার জন্য বাইনারি সার্চ ব্যবহার করা হয়। বাইনারি সার্চ লিস্টকে প্রতিটা ধাপে দুইভাগে ভাগ করে। এর ফলে খুব দ্রুত কোন কিছু খুঁজে বের করা সম্ভব হয়। আমরা যারা ডিকশনারির হার্ড কপি ব্যবহার করেছি, তারা মূলত এই বাইনারি সার্চ ব্যবহার করেই ডিকশনারি থেকে কোন শব্দ খুঁজে বের করেছি। ডিকশনারিতে শব্দ গুলো সর্ট করা থাকে। তাই আমরা নিজের অবচেতন মনেই বাইনারি সার্চ ব্যবহার করি।
বাইনারি সার্চের ধাপ গুলোঃ
- প্রথমে লিস্টের মাঝের ইনডেক্স বের করা হয়। যদি মাঝের ইনডেক্সে টার্গেট পাওয়া যায়, তাহলে ঐ মাঝের ইনডেক্স রিটার্ণ করবে।
- যদি মাঝের ইনডেক্সে টার্গেট না পাওয়া যায় এবং টার্গেট মাঝের ইনডেক্সের সংখ্যা থেকে ছোট হয়, তাহলে ইনডেক্সের বাম পাশের অংশে সার্চ করা হয়।
- যদি মাঝের ইনডেক্সে টার্গেট না পাওয়া যায় এবং টার্গেট মাঝের ইনডেক্সের সংখ্যা থেকে বড় হয়, তাহলে ইনডেক্সের ডান পাশের অংশে সার্চ করা হয়।
সাধারণত দুইটা পয়েন্টার যেমন left এবং righ পয়েন্টার ব্যবহার করা হয় মাঝের ইনডেক্স বের করার জন্য। এখানে left পয়েন্টার মানে হচ্ছে লিস্টের প্রথম ইনডেক্স এবং right পয়েন্টার মানে হচ্ছে লিস্টের শেষ ইনডেক্স। ধাপ গুলো পার করতে করতে যদি যদি left পয়েন্টার right পয়েন্টার থেকে বড় অথবা সমান হয়, তাহলে আমরা সার্চ করা বন্ধ করব। আরেকটু সুন্দর ভাবে বুঝার চেষ্টা করি। যেমন নিচের লিস্টটি দেখিঃ
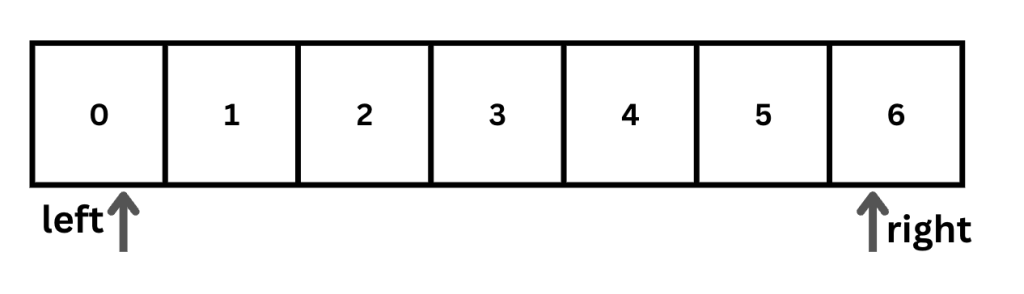
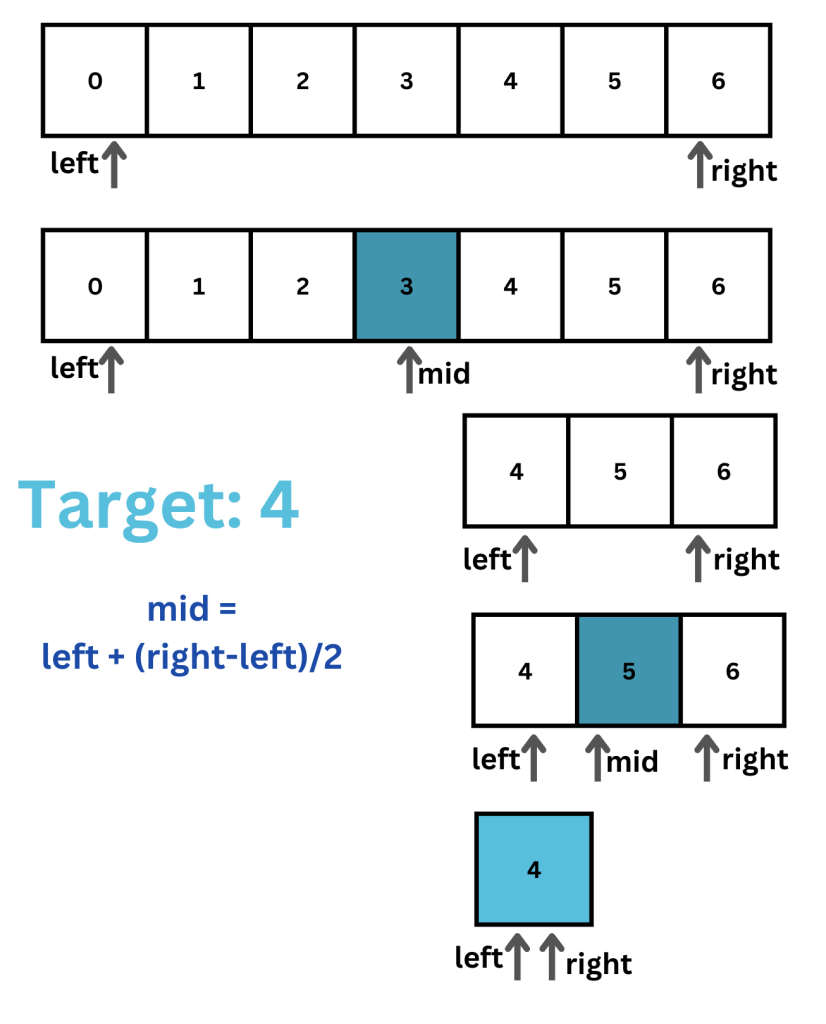
0, 1, 2, 3, 4, 5, 6 এই লিস্টে 4 আছে কিনা, তা খুঁজে বের করব।
লিস্টের প্রথম ইনডেক্সকে left এবং শেষ ইনডেক্সকে right ধরে দুইটা পয়েন্টার সেট করি। বুঝার সুবিধার্থে এখানে লিস্টের আইটেম এবং ইনডেক্স সংখ্যা একই রেখেছি।
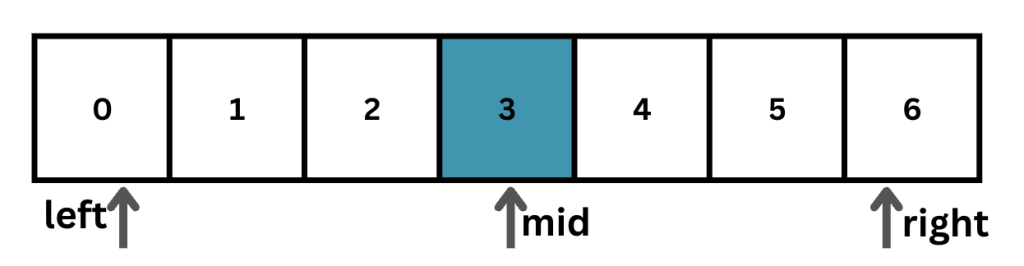
এরপর লিস্টের মধ্যের আইটেমটা বের করব এভাবেঃ mid = left + (right - left) / 2 । এই ক্ষেত্রে 0 + (6 – 0) / 2 = 6/ 2 = 3। এখানে left, right বা mid পয়েন্টার গুলো ইনডেক্স নাম্বার বুঝায়, লিস্টের আইটেম নয়।
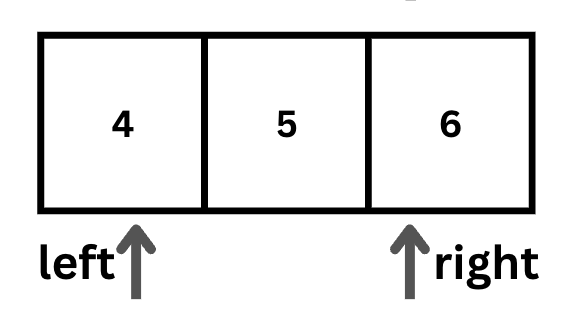
এখন যদি এই mid ইনডেক্সে 4 পেয়ে যাই, তাহলে এই mid ভ্যালুটা রিটার্ণ করব। মানে mid ইনডেক্সে 4 রয়েছে। যদি না হয়, তাহলে আমরা এই মিড পয়েন্টকে ধরে লিস্টকে দুই ভাগ করে নিতে পারি। যেহেতু এই উদাহরণে mid ইনডেক্সে 4 আইটেমটি নেই এবং এই 4 মিড পয়েন্টে থাকা 3 থেকে বড়, তাই আমরা মিড পয়েন্টের বামের অংস সার্চ এরিয়া থেকে বাদ দিব। আমরা লিস্টকে অর্ধেক করে নিব। তাহলে নতুন left ইনডেক্স হবে mid + 1। এই ক্ষেত্রে 4।
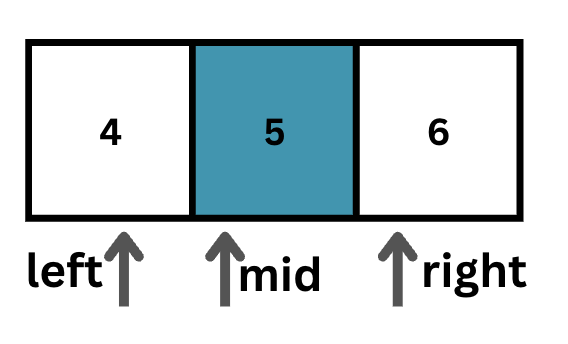
এই নতুন লিস্টের মিড পয়েন্ট বের করিঃ 4 + (6 - 4) / 2 = 5
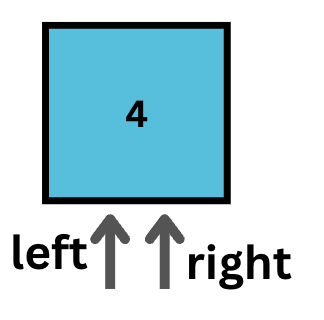
এখন আবার দেখব এই মিড ইনডেক্সে যেই সংখ্যাটা রয়েছে, তা কি আমাদের টার্গেট ভ্যালু 4 কিনা। যেহেতু এই মিডে রয়েছে 5 এবং আমাদের টার্গেট ভ্যালু হচ্ছে 4 যা এই 5 থেকে ছোট, তাই নতুন লিস্টের ডানের অংশ আমরা বাদ দিব। নতুন right ইনডেক্স হবে mid – 1 = 4।
এই সময় left এবং right একই ইনডেক্সে পয়েন্ট করবে। যদি ঐ ইনডেক্সে টার্গেট ভ্যালু 4 থাকে, তাহলে আমরা রিটার্ণ করব যে 4 পাওয়া গেছে। যদি না পাওয়া যায়, তাহলে প্রোগ্রাম জানাবে যে সংখ্যাটি লিস্টে পাওয়া যায় নি। উপরের উদাহরণে এই ধাপে এসে আমরা দেখেছি যে 4 নং ইনডেক্সে আমাদের টার্গেট ভ্যালু 4 পাওয়া গিয়েছে।
বুঝার সুবিধার্থে সব গুলো ধাপ একত্রেঃ
বাইনারি সার্চ অ্যালগরিদমের টাইম কমপ্লেক্সিটিঃ
যে কোন অ্যালগরিদমের টাইম কমপ্লেক্সিটি গুরুত্বপূর্ণ বিষয়। আমাদের জানা দরকার যে অ্যালগরিদমটি আমরা ব্যবহার করছি, তা কতটুকু রিসোর্স ব্যবহার করবে। বাইনারি সার্চের ক্ষেত্রে টাইম কমপ্লেক্সিটি হচ্ছে O(log n)। আর স্পেস কমপ্লেক্সিটি হচ্ছে O(1)। কারণ এখানে এক্সট্রা কোন মেমরি ব্যবহার করা লাগেনি।
বেশির ভাগ ইন্টার্ভিউতে বাইনারি সার্চ সম্পর্কিত সমস্যা সমাধান করতে দেওয়া হয়। যারা জব করার জন্য প্রিপারেশন নিচ্ছেন, তারা চাইলে লিটকোডে বাইনারি সার্চ সম্পর্কিত কিছু সমস্যা সমাধান করতে পারেন। যেমন শুধু উপরের অ্যালগরিদমটা ইমপ্লিমেন্ট করলেই 704. Binary Search সমস্যাটা সমাধান করতে পারবেন। অন্যান্য বাইনারি সার্চ সম্পর্কিত সমস্যা গুলোঃ Binary Search। এছাড়া এই লেখাটিও দেখতে পারেনঃ Powerful Ultimate Binary Search Template.
বাইনারি সার্চ অ্যালগরিদমের ইমপ্লিমেন্টেশনঃ
বাইনারি সার্চ অ্যালগরিদম দুইভাবে ইমপ্লিমেন্ট করা যায়।
- ইটারেটিভ এপ্রোচ
- রিকার্সিভ এপ্রোচ
ইটারেটিভ এপ্রোচঃ
def binary_search(nums, target):
left = 0
right = len(nums) - 1
# repeat until left & right meet
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif target < nums[mid]:
right = mid - 1
else:
left = mid + 1
return -1
result = binary_search([3, 4, 5, 6, 7, 8, 9], 7)
if result != -1:
print("Target is at index: " + str(result))
else:
print("Target not found in the list")
var nums = [-1,0,3,5,9,12]
var target = 9
var left = 0
var right = nums.count - 1
while left < right {
let mid = left + ( right - left ) / 2
if nums[mid] == target{
print("Found target at \(mid)th index.")
break
} else if (nums[mid] < target){
left = mid + 1
} else if ( nums[mid] > target){
right = mid - 1
}
}
// Output: Found target at 4th index.
রিকার্সিভ এপ্রোচ
def binarySearch(nums, target, left, right):
if right >= left:
mid = left + (right - left)//2
# If found at mid, then return it
if nums[mid] == target:
return mid
# Search the left half
elif nums[mid] > target:
return binarySearch(nums, target, left, mid-1)
# Search the right half
else:
return binarySearch(nums, target, mid + 1, right)
else:
return -1
nums = [-1,0,3,5,9,12]
target = 9
result = binarySearch(nums, target, 0, len(nums)-1)
if result != -1:
print("Found target at index " + str(result))
else:
print("Not found")
func binarySearch(_ array: [Int], key: Int, left: Int, right: Int) -> Int? {
// Base case: key not found
if left > right {
return nil
}
let mid = left + (right - left) / 2
if array[mid] == key {
return mid // Base case: key found
} else if array[mid] < key {
// Search in the upper half
return binarySearch(array, key: key, left: mid + 1, right: right)
} else {
// Search in the lower half
return binarySearch(array, key: key, left: left, right: mid - 1)
}
}
// Example usage
let numbers = [-1, 0, 3, 5, 9, 12]
if let index = binarySearch(numbers, key: 9, left: 0, right: numbers.count) {
print("Found 9 at index \(index)")
} else {
print("9 not found in the array")
}
// Output: Found 9 at index 4