পাইথন মার্জ সর্ট

খুবি জনপ্রিয় একটা সর্টিং অ্যালগরিদম হচ্ছে মার্জ সর্ট। এটি ডিভাইড এবং কনকার অ্যালগরিদম স্ট্রেটেজি ফলো করে কোন লিস্ট সাজিয়ে দেয়।

ডিভাইড এবং কনকার স্ট্রেটেজিঃ

ডিভাইড এবং কনকার স্ট্রেটেজিতে একটা বড় সমস্যাক ছোট ছোট ভাগে ভাগ করা হয়। এরপর ঐ ছোট ছোট অংশ গুলোকে সবার আগে সমাধান করা হয়। পরিশেষে সমাধানকৃত ছোট অংশ গুলো একত্র করে পূর্নাঙ্গ সমাধান দেয়।

ডিভাইড এবং কনকার অ্যালগরিদমের স্টেপ গুলোঃ

• Divide: রিকার্শন ব্যবহার করে সমস্যা গুলোকে ছোট ছোট অংশে ভাগ করা হয়।
• Conquer: সাব-প্রবলেম গুলোকে রিকার্শনের মাধ্যমে সমাধান করা হয়।
• Combine: সাব-প্রবলেমের সমাধান গুলো একত্র করে পূর্নাঙ্গ সমাধান আউটপুট দেওয়া হয়।

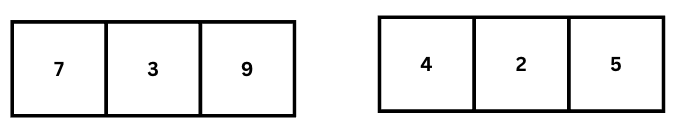
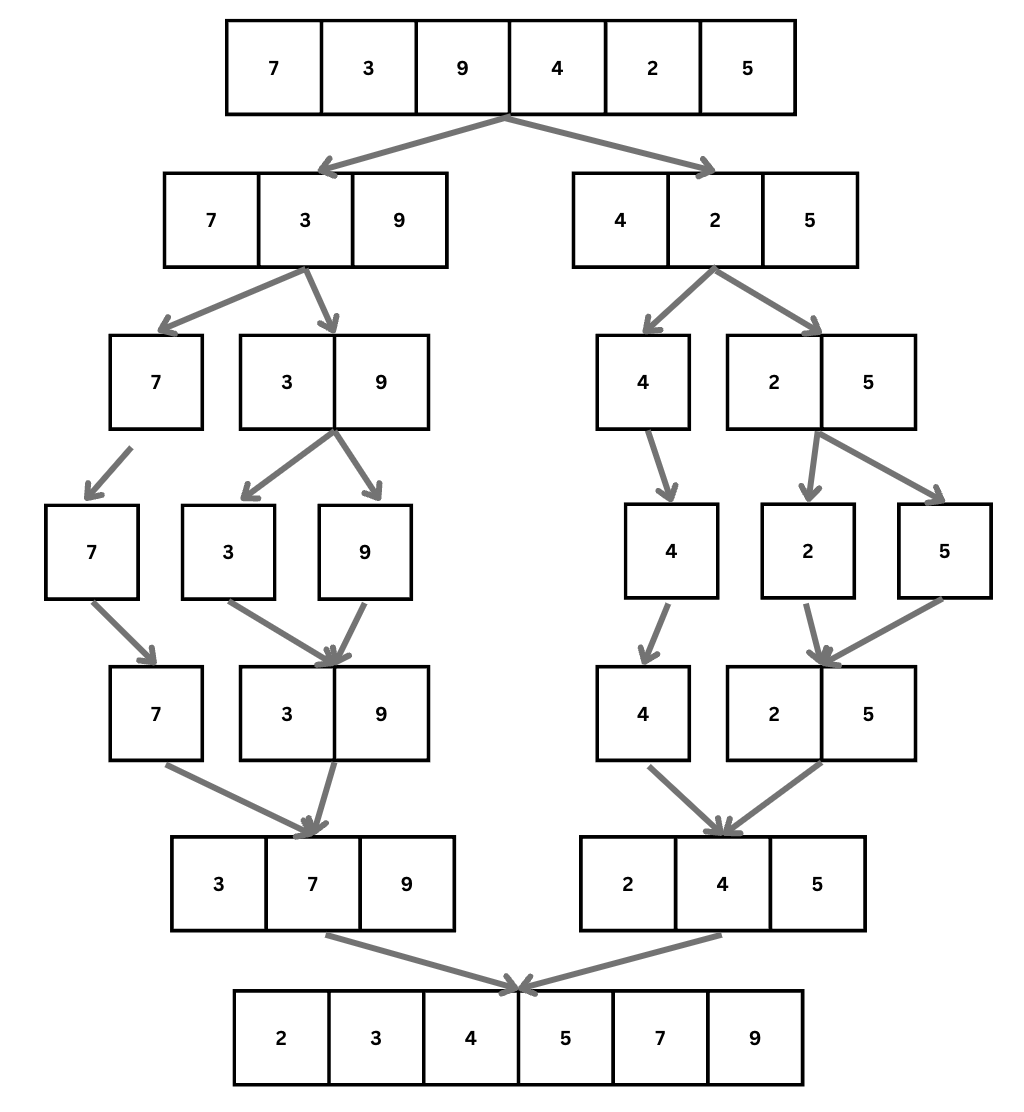
মার্জ সর্ট এই ডিভাইড এবং কনকার স্ট্রেটেজি ফলো করে।  মার্জ সর্ট কিভাবে কাজ করে, তা একটা উদাহরণের মাধ্যমে বোঝার চেষ্টা কড়ই। উদাহরণ হিসেবে 7, 3, 9, 4, 2, 5 এই লিস্টকে ব্যবহার করি।

মার্জ সর্ট প্রথমে এই লিস্টকে সমান দুই ভাগে ভাগ করবে। এখন প্রশ্ন আসতে পারেন, সমান ভাগে দুই ভাগ করা না গেলে কি করব? পরের ধাপে দেখছি তা।

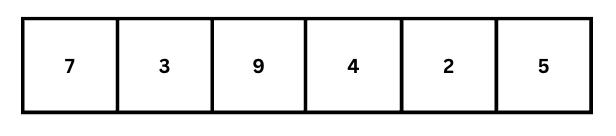
এই ধাপে এসে দেখছি প্রতিটা ভাগে তিনটে করে ইলিমেন্ট রয়েছে। সমান ভাগে দুই ভাগ করা যাবে না। ভাগ যে কোন স্ট্রেটেজি ফলো করেই করা যাবে। যেমন যদি লিস্টে ইলিমেন্ট সংখ্যা হয় n, তাহলে এক পাশে n/2 এর ফ্লোর ডিভিশন সংখ্যক ইলিমেন্ট নিতে পারি। আরেক পাশে নিতে পারি n/2+1। পাইথনে এই জিনিসটা সহজে ফ্লোর ডিভিশন ব্যবহার করে করা যায়। 3/2 এর ফ্লোর ডিভিশন হবে 1। তাহলে এক পাশে নিব 1 টা ইলিমেন্ট, অন্য পাশে নিব 1+1 মানে দুইটা ইলিমেন্ট। নিচের মত করেঃ

 

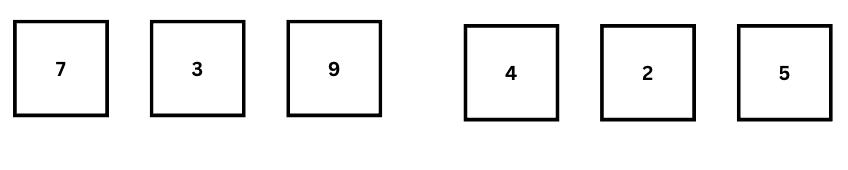
এই ধাপে এসে দেখছি যে দুইটা লিস্টে একটা করে ইলিমেন্ট রয়েছে। 7 এবং 4।  যে লিস্টে একটা করে ইলেমেন্ট রয়েছে, তাকে আর ভাগ করা লাগবে না। এটাকে বলে এটমিক স্টেট। যে লিস্ট গুলো এটমিক স্টেটে নেই, সেগুলোকে আরো ভাগ করতে হবে নিচের মত করেঃ

সব গুলোকে ভাগ করার পর লিস্টের সব গুলো লিস্টই এটমিক স্টেটে পৌঁছেছে।  মানে এ লিস্ট গুলোকে আর ভাগ করা যাবে না।

আমরা খেয়াল করে দেখব লিস্টকে সাব লিস্টে পরিবর্তন করার সময় অন্য কোন অপারেশন করা হয়নি। শুধু মাত্র ছোট ছোট লিস্টে ভাগ করা হয়েছে। এই অবস্থায় বলা যায় প্রতিটা লিস্টই সর্টেড অবস্থায় রয়েছে। যেমন 7 যে লিস্টে রয়েছে, সেখানে একটাই ইলিমেন্ট 7 রয়েছে, এবং এটি সর্টেড।

এবারের কাজ হচ্ছে মার্জ করা। মার্জ করার ক্ষেত্রে ঠিক যে অর্ডারে আমরা লিস্টকে সাব লিস্টে ভাগ করেছি, ঠিক একই অর্ডারে মার্জ করতে হবে। দুইটা সাব লিস্ট মার্জ করার ক্ষেত্রে লিস্ট দুইটা কম্পেয়ার করে করে যে আইটেম ছোট, তা মার্জ লিস্টে প্রথমে রাখতে হবে।

মার্জের প্রথম ধাপে প্রথমে 3 এবং 9 কে মার্জ করতে হবে। কারণ ভাগ করার সময় সবার শেষে 3 এবং 9 কে ভাগ করেছি। এখানে 3 এবং 9 এর মধ্যে তুলনা করে দেখলে দেখা যাবে ৩ ছোট। তাই মার্জ লিস্টে প্রথমে 3 এবং পরে 9 রাখতে হবে। একই ভাবে 2 এবং 5 এর মধ্যে 2 ছোট, তাই 2 আগে এবং 5 পরে রাখব।  প্রথম মার্জের পর পাবোঃ

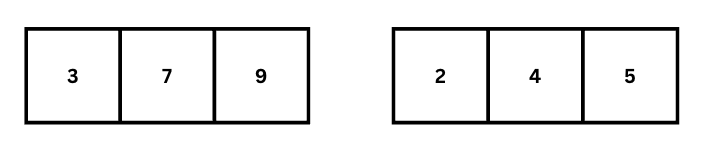
মার্জের পরের ধাপে [7] এবং [3,9] লিস্ট দুইটা মার্জ করতে হবে। এই ক্ষেত্রে এই দুইটা লিস্ট এর মধ্যে প্রতিটা আইটেম তুলনা করে যে আইটেম ছোট, সেটি মার্জ লিস্টের শুরুতে রাখতে হবে। যেমন প্রথমে 7 এবং 3 এর তুলনা করা হবে। যেহেতু 3 ছোট, তাই মার্জ লিস্টের শুরুতে 3 বসবে। এরপর 7 এবং 9 এর তুলনা করবে। এখানে 7 ছোট, তাই 7 আগে বসবে। 9 এর সাথে তুলনা করার মত আর কোন সংখ্যা নেই, তাই এরপর 9 বসে যাবে। একই ভাবে অপর পাশের [4] এবং [2,5] ও মার্জ হবে। দ্বিতীয় ধাপে সাব লিস্ট গুলোকে মার্জ করার পর পাবোঃ

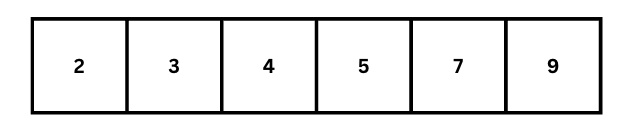
এই ধাপে দুইটা সাব লিস্ট পাবো। এবং এগুলো মার্জ করার পর  আমরা সর্টেড লিস্ট পাবো। [3,7,9] এবং [2,4,5] এই দুইটা লিস্টই সর্টেড। দুইটা এক সাথে মার্জ  করার ক্ষেত্রে প্রতিটা আইটেমের সাথে প্রতিটা আইটেমের তুলনা করা হবে। যেমন 3 এবং 2 এর মধ্যে 2 ছোট, তাই 2 মার্জ লিস্টের শুরুতে বসবে। এরপর তুলনা করে দেখব 3 থেকে ছোট আর কোন সংখ্যা নেই, তাই 3 বসে যাবে। তারপর 7 এবং 4 এর মধ্যে তুলনা করে দেখলে দেখব 4 ছোট, তাই 4 আগে বসবে। এরপর 7 এবং 5 এর মধ্যে তুলনা করে দেখবে 5 ছোট, তাই 5 আগে বসবে। এরপর 7 নিজে বসবে। শুধু মাত্র 9 থাকবে, যেহেতু আর কোন সংখ্যা নেই তুলনা করার মত, তাই সবার শেষে 9 বসবে। সর্বশেষ রেজাল্টঃ

 

 

এই পুরো প্রসেসটা একত্রে দেখলে  নিচের মত দেখবঃ

 

 

 

মার্জ সর্ট বুঝার সবচেয়ে সহজ উপায় হচ্ছে নিজে নিজে একটা লিস্ট নিয়ে তারপর উপরের স্টেপ গুলো খাতা কলমে নিজে নিজে একে ফেলা। খাতা কলমে এই স্টেপ গুলো করতে গিয়ে মনে হবে মার্জ সর্ট অনেক সহজ। আমাদের স্বতঃস্ফূর্ত জ্ঞান দিয়েই সমাধান করে ফেলা যায়।  আর ধাপ গুলো কোড আকারে লিখলেই মার্জ সর্টের প্রোগ্রাম লেখা হয়ে যাবে।

মার্জ সর্টের তিনটা প্রধান অংশ রয়েছেঃ

• একটা লিস্টকে দুইটা সাব-লিস্টে ভাগ করা
• দুইটা সর্টেড লিস্টকে মার্জ বা একত্র করা
• মার্জ সর্ট

বুঝার সুবিদার্থে এই তিনটা অংশ আলাদা আলাদা করে লিখেছি নিচে। যেমন স্প্লিট ফাংশনঃ

def split(input_list):
    midpoint = len(input_list) // 2
    return input_list[:midpoint], input_list[midpoint:]
print (split([7,3,9,4,2,5]))

যা আউটপুট দিবেঃ

([7, 3, 9], [4, 2, 5])

দুইটা সর্টেড লিস্ট মার্জ করার ফাংশনঃ

def merge_sorted_lists(list_left, list_right):

    index_left = index_right = 0
    list_merged = []  
    list_len_target = len(list_left) + len(list_right)
    while len(list_merged) < list_len_target:
        # if left item is smaller
        if list_left[index_left] <= list_right[index_right]:
            list_merged.append(list_left[index_left])
            index_left += 1
        # right item is smaller
        else:
            list_merged.append(list_right[index_right])
            index_right += 1
            
        # if reached the end of right
        if index_right == len(list_right):
        
            list_merged += list_left[index_left:]
            break
        # if reached the end of left    
        elif index_left == len(list_left):
            list_merged += list_right[index_right:]
            break
        
    return list_merged

print(merge_sorted_lists([7],[3,9]))

যা আউটপুট দিবেঃ

[3, 7, 9]

মার্জ সর্টে আমরা উপরের দুইটা ফাংশন ব্যবহার করব। মার্জ সর্টের রিকার্সিভ ফাংশনঃ

def merge_sort(input_list):
    if len(input_list) <= 1:
        return input_list
    else:
        left, right = split(input_list)
        # recursively call merge_sort 
        return merge_sorted_lists(merge_sort(left), merge_sort(right))

সম্পূর্ণ প্রোগ্রামঃ

# split a list into 2 sub list 
def split(input_list):
    midpoint = len(input_list) // 2
    return input_list[:midpoint], input_list[midpoint:]

# merge 2 sorted list 
def merge_sorted_lists(list_left, list_right):

    index_left = index_right = 0
    list_merged = []  
    list_len_target = len(list_left) + len(list_right)
    while len(list_merged) < list_len_target:
        # if left item is smaller
        if list_left[index_left] <= list_right[index_right]:
            list_merged.append(list_left[index_left])
            index_left += 1
        # right item is smaller
        else:
            list_merged.append(list_right[index_right])
            index_right += 1
            
        # if reached the end of right
        if index_right == len(list_right):
        
            list_merged += list_left[index_left:]
            break
        # if reached the end of left    
        elif index_left == len(list_left):
            list_merged += list_right[index_right:]
            break
        
    return list_merged
# merge sort 
def merge_sort(input_list):
    if len(input_list) <= 1:
        return input_list
    else:
        left, right = split(input_list)
        # recursively call merge_sort 
        return merge_sorted_lists(merge_sort(left), merge_sort(right))

print(merge_sort([7,3,9,4,2,5]))

যা আউটপুট দিবেঃ

[2, 3, 4, 5, 7, 9]