গ্রাফ থিওরি, গ্রাফের রিপ্রেজেন্টেশন এবং ইমপ্লিমেন্টেশন

গ্রাফঃ গ্রাফ হচ্ছে কত গুলো নোড (Node) বা ভার্টেক্স(vertice)  এবং এজের (Edge) সমষ্টি। নিচে একটি গ্রাফের ছবি দেওয়া হলোঃ

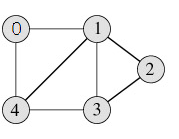
এ গ্রাফে পাঁচটি নোড বা ভার্টেক্স রয়েছে। নোড গুলো হচ্ছেঃ 0,1,2,3,4,5. আর উপরের গ্রাফে এজ রয়েছে ৭টি। নোড গুলোর সংযোগ কারী রেখা হচ্ছে এজ।

 

গ্রাফকে নিচের মত করে ভাগ করা যায় :

1. Directed, weighted edges
2. Directed, unweighted edges
3. Undirected, weighted edges
4. Undirected, unweighted edges

 

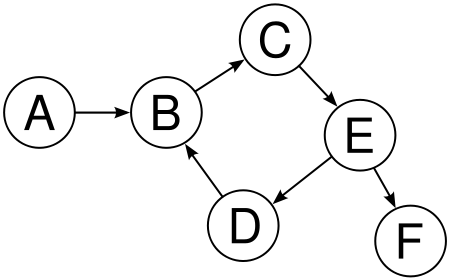
ডিরেক্টেড গ্রাফঃ যে  গ্রাফের এজ গুলো যদি তীর চিহ্ন দিয়ে চিহ্নিহিত থাকে, তাকে ডিরেক্টেড গ্রাফ বলে। নিচের গ্রাফটই একটি ডিরেক্টেড গ্রাফ।

আনডিরেক্টেড গ্রাফঃ গ্রাফের এজ গুলোতে যদি কোন তীর চিহ্ন না থাকে, সে গুলো হচ্ছে আনডিরেক্টেড গ্রাফ। আনডিরেক্টেড গ্রাপ দ্বিমুখী বা Bidirectional গ্রাফ নামেও পরিচিত।

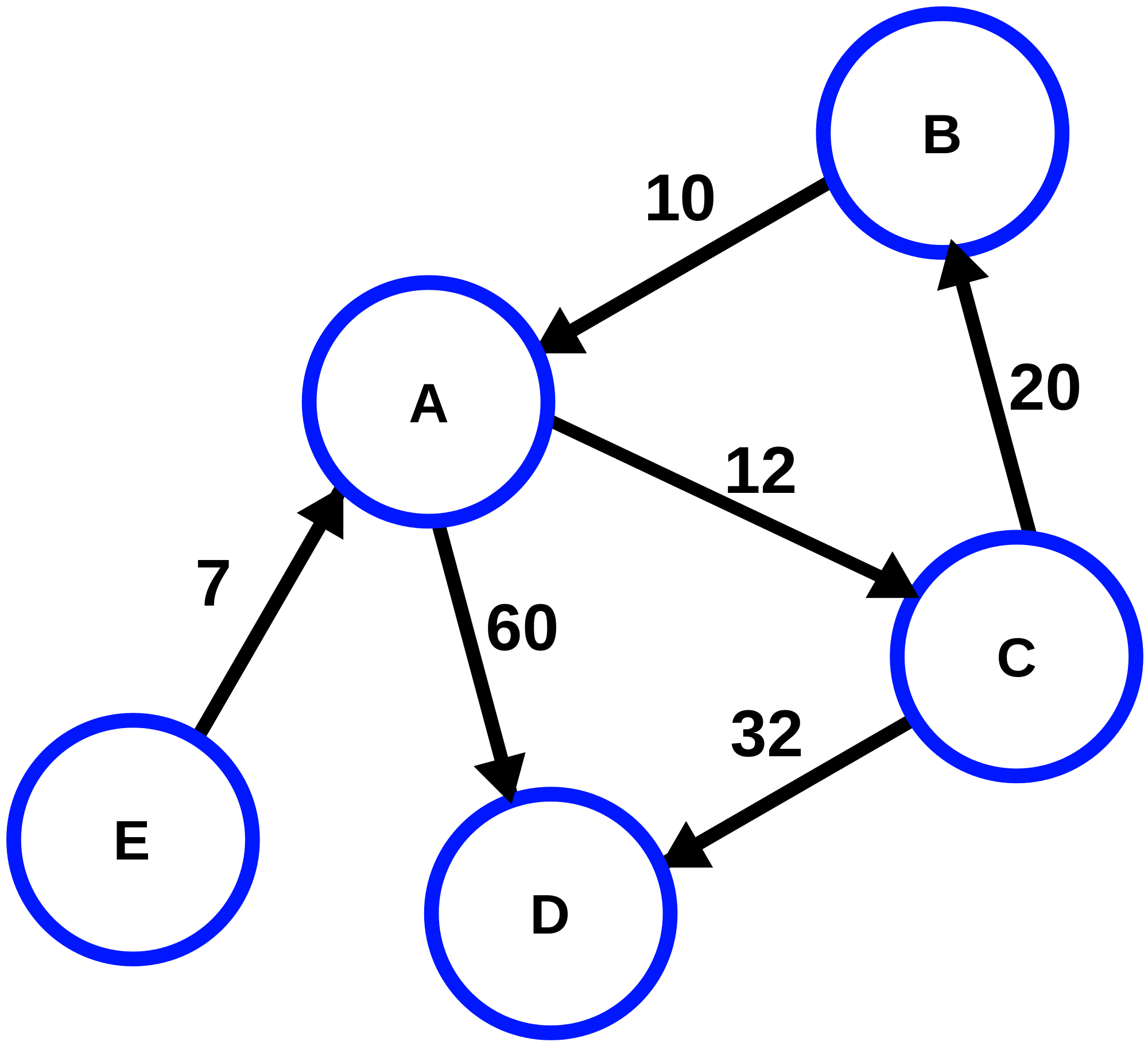
ওয়েটেড গ্রাফঃ একটা নোড থেকে আরেকটা নোডের কস্ট উল্যেখ থাকলে যে গ্রাফকে ওয়েটেড গ্রাফ বলে।

আনওয়েটেড গ্রাফঃ একটা নোড থেকে আরেকটা নোডের কস্ট উল্যেখ না থাকলে যে গ্রাফকে আনওয়েটেড গ্রাফ বলে।

 

অ্যাডজেসেন্ট ভার্টেক্স: একটা ভার্টেক্স যদি আরেকটা ভার্টেক্সের সাথে এজ দ্বারা কানেক্টেড থাকে তাহলে বলা হয় একটা আরেকটার অ্যাডসেসেন্ট ভার্টেক্স।

যেমন উপরের গ্রাফে 0 কানেক্টেড আছে 1 এবং 4 এর সাথে। তাহলে 1 এবং 4 হচ্ছে 0 এর  অ্যাডজেসেন্ট ভার্টেক্স এক টা ভার্টেক্সের একের অধিক অ্যাডজেসেন্ট ভার্টেক্স থাকতে পারে। যেমন উপরের গ্রাফে 1 এর অনেক গুলো অ্যাডজেসেন্ট ভার্টেক্স, সেগুলো হচ্ছেঃ 0, 4, 3 এবং 2.

 

গ্রাফ রিপ্রেজেন্টেশনঃ

গ্রাফ দিয়ে অনেক ধরনের সমস্যা সমাধান করা যায়। কি ধরনের সমস্যা সমাধান করা যায়, লেখার শেষে বলব। সমস্যা গুলো সমাধান করার জন্য আমাদের গ্রাফটি কম্পিউটাকে বুঝাতে হবে। কম্পিউটারকে একটা গ্রাফের ছবি দিলে সে বুঝবে না। আর বুঝানোকে বলা হয় গ্রাফ রিপ্রেজেন্টেশন। দুইটা প্রধান উপায় হচ্ছেঃ

1. অ্যাডজেসেন্সি ম্যাট্রিক্স।
2. অ্যাডজেসেন্সি লিস্ট।

 

একটি 2D অ্যারে দিয়ে অ্যাডজেসেন্সি ম্যাট্রিক্স রিপ্রেজেন্ট করা হয়। অ্যারের সাইজ হচ্ছে V*V। এখানে V মানে গ্রাফের টোটাল ভার্টেক্স সংখ্যা। যেমন উপরের গ্রাফে রয়েছে ৫টি ভার্টেক্স। তাহলে আমাদের অ্যারের সাইজ হবে 5*5. অ্যারের ইন্ডেক্স শূণ্য থেকে শুরু হয়। ধরে নিচ্ছিল অ্যারে এর নাম adj, তাহলে অ্যারেটি হবে adj[4][4]

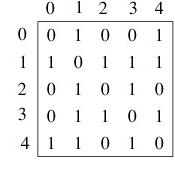
উপরের গ্রাফটের অ্যাডজেসেন্সি ম্যাট্রিক্স রূপ হবে নিচের মত করেঃ

একটা ভার্টেক্সের সাথে যদি একটা ভার্টেক্স কানেকটেড থাকে, তাহলে ঐ অ্যারের ঐ ঘরে একটা 1 বসবে। আর যদি কানেকটেড না থাকে, তাহলে বসবে 0.

অ্যারেটি যদি adj[][] হয়, i এবং j ভার্টেক্স যদি কানেক্টেড থাকে একটা এজ দিয়ে, তাহলে adj[i][j] = 1

আমরা অ্যারের সব গুলো ঘরে ০ বসিয়ে দিব। তারপর যেটার সাথে যেটা কানেক্টেড ঐ অ্যারের ঐ ঘরে আমরা একটা 1 বসিয়ে দিবে।

 

	0	1	2	3	4
0	0	0	0	0	0
1	0	0	0	0	0
2	0	0	0	0	0
3	0	0	0	0	0
4	0	0	0	0	0

 

উপরের গ্রাফে দেখি 0 এবং 1 কানেক্টেড, তাই adj[0][1] = 1 বসেছে। 0 এবং 1 কানেক্টেড যে কথা, 1 এবং 0 কানেক্টেড ও একই কথা। তাই adj[1][0] এ ওa 1 বসেছে।

	0	1	2	3	4
0	0	1	0	0	0
1	1	0	0	0	0
2	0	0	0	0	0
3	0	0	0	0	0
4	0	0	0	0	0

 

1 কানেক্টেড হচ্ছে  0, 2, 3 এবং 4 এর সাথে। adj[1][0] =  1 আগেই বসিয়ে নিয়েছি বসেছে। তাহলে adj[1][2], adj[1][3], adj[1][4] এ গুলোতে 1 বসিয়ে দিব। adj[i][j] = adj[j][i], তাই একই ভাবে adj[2][1], adj[3][1], adj[4][1] এও আমরা 1 বসিয়ে দিব।তাহলে আমাদের ম্যাটিক্সটি হবেঃ

 

	0	1	2	3	4
0	0	1	0	0	0
1	1	0	1	1	1
2	0	1	0	0	0
3	0	1	0	0	0
4	1	0	0	0	0

 

এভাবে বাকি গুলো পূরণ করলে আমাদের অ্যারে / ম্যাটিক্সটি হবেঃ

	0	1	2	3	4
0	0	1	0	0	1
1	1	0	1	1	1
2	0	1	0	1	0
3	0	1	1	0	1
4	1	1	0	1	0

 

এটা যেহেতু একটা অ্যারে, প্রোগ্রামিং এ আমরা কিভাবে অ্যারে তৈরি করতে হয়, তা জানি।

 

আমরা একটা সি প্রোগ্রামে রিপ্রেজেন্ট করতে পারি এভাবেঃ

অ্যারের ইন্ডেক্স সহঃ

 

 

আমরা যখন প্রোগ্রাম লিখব, তখন তো আমরা জানব না গ্রাফের ভার্টেক্স কয়টা, এজ কয়টা। কোনটার সাথে কোনটা কানেক্টেড। তখন আমাদেরকে ব্যবহারকারী থেকে ইনপুট নিতে হবে। তার জন্যঃ

অ্যাডজেসেন্সি ম্যাটিক্স রিপ্রেজেন্টেশন সহজ। ছোট খাটো গ্রাফ রিপ্রেজেন্টেশনের জন্য সুবিধে। সমস্যা হচ্ছে যখন বড় সড় গ্রাফ নিয়ে কাজ করব, তখন এটা তেমন এফিশিয়েন্ট না। প্রোগ্রামারদের সবার আগে যেটা চিন্তা করতে হয়, তা হচ্ছে এফিশিয়েন্সি। যেমন আমরা একটা বিমান কম্পানির জন্য একটা প্রোগ্রাম বানাবো। বিভিন্ন শহরে যাওয়ার সহজ রাস্তা বের করার প্রোগ্রাম লিখতে হবে। তখন আমাদের অনেক গুলো শহর নিয়ে কাজ করতে হবে। যেমন ১০,০০০ টি শহর আছে এবং একটা থেকে আরেকটাতে যেতে ৫০,০০০ পথ রয়েছে। এখন আমরা যদি অ্যাডজেসেন্সি ম্যাটিক্স দিয়ে রিপ্রেজেন্ট করি, তাহলে আমাদের 10,000×10,000  সাইজের একটা অ্যারে ডিক্লেয়ার করতে হবে। যা কম্পিউটারে বিশাল জায়গা দখল করে বসে থাকবে।  কিন্তু যার বেশির ভাগই আমাদের দরকার হবে না। আর এই সমস্যা সমাধান করার জন্য আমরা ব্যবহার করব অ্যাডজেসেন্সি লিস্ট।

 

অ্যাডজেসেন্সি লিস্টঃ

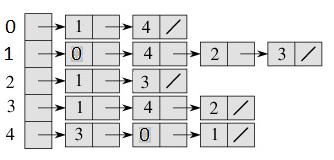
আমাদের উপড়ের গ্রাফটি যদি অ্যাডজেসেন্সি লিস্ট দিয়ে রিপ্রেজেন্ট করি, তাহলে দেখতে নিচের মত হবেঃ

এখানে দেখি যে 0 এর সাথে কানেক্টেড হচ্ছে 1 & 4। যে নোডের সাথে যে নোড কানেক্টেড, আমরা শুধু সে গুলোই লিখেছি। এভাবে বাকি নোড গুলোও। এতে আমাদের অনেক গুলো মেমরি সেভ হচ্ছে।

 

অ্যাডজেসেন্সি লিস্ট রিপ্রেজেন্ট করার জন্য আমরা লিঙ্কড লিস্টের একটা অ্যারে ব্যবহার করি। তা অ্যাডজেসেন্সি লিস্ট লিস্ট রিপ্রেজেন্ট করতে চাইলে আগে লিঙ্কড লিস্ট সম্পর্কে পরিষ্কার ধারণা থাকা দরকার। নিচের লিঙ্ক থেকে লিঙ্কড লিস্ট সম্পর্কে বিস্তারিত জানা যাবেঃ

• লিঙ্কড লিস্ট / Linked list সম্পর্কে ধারণা এবং সি প্রোগ্রামিং এ ইমপ্লিমেন্টেশন

লিঙ্কড লিস্ট সম্পর্কে জানার পড় আমরা নিজেরা অ্যাডজেসেন্সি লিস্ট ইমপ্লেমেন্ট করতে পারি। প্রথমে নিজে চেষ্টা করব। এর পর না পারলে এখান থেকে দেখতে পারিঃ Graph and its representations। অ্যাডজেসেন্সি লিস্ট এর ইমপ্লিমেন্টেশন দেওয়া রয়েছে। এই লেখাতে ব্যবহৃত কয়েকটি ইমেজ উপরের আর্টিকেল থেকে নেওয়া হয়েছে। আর কিছু ইমেজ নেওয়া হয়েছে উইকিপিডিয়া থেকে।