অ্যালগরিদম, কমপ্লেক্সিটি এনালাইসিস ও নোটেশন

অ্যালগরিদম হচ্ছে কোন একটি কাজ করার স্টেপ গুলো। প্রতিদিনই আমরা শত শত অ্যালগরিদম ব্যবহার করছি, নিজেদের অজান্তেই। বাসা থেকে স্কুলে যাবো? কোন রাস্তা দিয়ে গেলে সময় সবচেয়ে কম লাগবে, তা চিন্তা করি। এটাও একটা অ্যালগরিদম।

কম্পিউটার আবিষ্কারের আগেও অ্যালগরিদম ছিল। যদিও এখন আমরা অ্যালগরিদম বলতে কম্পিউটার সাইন্স এর একটা সাবজেক্ট বুঝি। মূলত এটি গণিতের একটা শাখা। সহজে বলতে গেলে অ্যালগরিদম হচ্ছে কোন একটা সমস্যার সমাধানের গাণিতিক পদ্ধতি। একটা অ্যালগরিদম ইনপুট হিসেবে কিছু ডেটা বা প্যারামিটার নিবে। এরপর প্রয়োজনীয় কম্পিউটেশন শেষে রিটার্ন হিসেবে কিছু আউটপুট দিবে।

সিম্পল একটা সমস্যা দিয়েই শুরু করি। লিনিয়ার সার্চ অ্যালগরিদম দিয়ে শুরু করতে পারি। আমাদের কাছে একটা লিস্ট আছে, যেখানে কিছু নাম্বার রয়েছে। আমরা এখন ঐ লিস্টে একটা নাম্বার আছে কিনা, তা বের করব। লিনিয়ার সার্চ করে কি, লিস্টের প্রথম নাম্বারটা নিবে, ঐটার সাথে যে নাম্বারটি খুঁজে বের করতে চাচ্ছি, তার সাথে মিলিয়ে দেখবে। যদি না মিলে, তাহলে লিস্টের পরের সংখ্যার সাথে মিলিয়ে দেখবে। যখন মিল পাবে, তখন লিস্টের ইনডেক্সটা রিটার্ন করবে। মানে কত তম ইনডেক্সে নাম্বারটা পাওয়া গিয়েছে, সেই ইনডেক্স। নিচের ইমেজটা দেখি। লিনিয়ার সার্চ যেভাবে কাজ করে, তার ভিজুয়াল চিত্র।

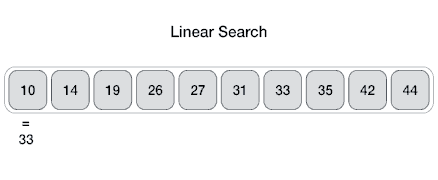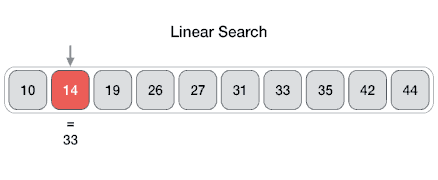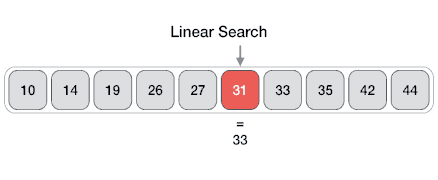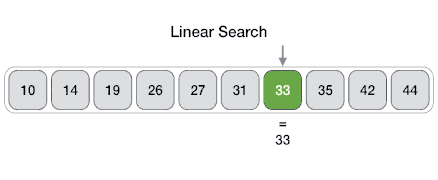
যদি এটাকে সুডোকোডে লিখি, এভাবে লেখা যায়ঃ

সুডোকোড সম্পর্কে একটু বলে নেই আগে। Pseudocode সত্যিকারের কোন প্রোগ্রামিং ল্যাঙ্গুয়েজের কোড না। কম্পিউটার ল্যাঙ্গুয়েজের কাছাকাছি এবং মানুষে পড়ে স্টেপ গুলো যেন সহজেই বুঝতে পারে, এমন কোড। এগুলোর নির্দিষ্ট কোন নিয়ম নেই। আর তাই হয়তো আপনি এক জায়গায় এক একটা অ্যালগরিদমের সুডোকোড এক এক রকম দেখতে পাবেন। ভালো করে লক্ষ্য করলে দেখা যাবে একটা অ্যালগরিদমের জন্য সব গুলো সুডোকোডের স্ট্রাকচার মোটামুটি একই রকম। আর সুডোকোড দেখে যে কোন ল্যাঙ্গুয়েজে সহজেই যে কোন অ্যালগরিদম ইমপ্লিমেন্ট করা যায়। আরো সহজ করে যদি বলি, কোন অ্যালগরিদমের ধাপ গুলো কম্পিউটার ল্যাঙ্গুয়েজের কাছা কাছি ভাষায় লিখে ফেলা, যেন পরবর্তীতে যে কোন ল্যাঙ্গুয়েজে ইমপ্লিমেন্ট করতে সহজ হয়।

linear_search (list, value)
    for each item in the list
        if match item == value
            return the item's location
        end if
    end for
end 

লিস্টে একটি নাম্বার রয়ছে কিনা, তা বের করার জন্য আমরা লিনিয়ার সার্চ অ্যালগরিদম ব্যবহার করেছি। এখন এক একটা সমস্যা একাধিক ভাবে সমাধান করা যায়। মানে একটা সমস্যা সমাধান করার অনেক গুলো অ্যালগরিদম থাকতে পারে। আমরা কোন অ্যালগরিদমটা ব্যবহার করব? কোন অ্যালগরিদম সিলেক্ট করার আগে আমরা অনেক হিসেব নিকেশ করি। পসিবল সব গুলো অ্যালগরিদম চিন্তা করি। কোন অ্যালগরিদম কত সময় নিবে, কতটুকু মেমরি নিবে তা দেখি। এসবকে বলে কমপ্লেক্সিটি এনালাইসিস। এরপর যে অ্যালগরিদম যত কম রিসোর্স নিবে, আমরা সেটাই ব্যবহার করি।

যেমন আমরা যে নাম্বারটি খুঁজব, তা অ্যারের প্রথম নাম্বারের সাথে মিলিয়ে দেখবে। যদি দেখে দুইটা একই নাম্বার, তাহলে অ্যারের কোন ইনডেক্সে নাম্বারটি রয়েছে, তা রিটার্ন করবে। সি, সি++ বা এই ধরণের ল্যাঙ্গুয়েজে মূল অ্যালগরিদমটা এভাবে ইমপ্লিমেন্ট করতে পারিঃ

for (i=0; i<n; i++)
    if (arr[i] == x)
    return i;

এখানে অ্যারে ইনিশিয়ালাইজেশন, কোন নাম্বারটি খুঁজে বের করা হবে, তা সেট করা ইত্যাদি সম্পর্কে লেখা হয় নি। অ্যালগরিদমটির জন্য যতটুকু দরকার, ততটুকু লেখা হয়েছে। কোন অ্যালগরিদমের কমপ্লিক্সিটি বের করার জন্য আমরা আগে বের করি ঐ অ্যালগরিদমটা প্রয়োগ করলে তা রান করতে কম্পিউটারের কয়টা ইন্সট্রাকশন লাগে।

Instruction Counting:

এক এক কম্পিউটারে এক একটা অপারেশন করতে এক এক টাইম লাগবে। যেমন অনেক পুরাতন লো কনফিগারেশন কোন কম্পিউটারে উপরের কোড অনেক স্লো কাজ করবে। আবার নতুন হাই কনফিগারেশন কম্পিউটারে অনেক দ্রুত বের করে ফেলবে। এই সমস্যা সমাধান করার জন্য আমরা কোন অ্যালগরিদম এনালাইসিস করার জন্য কিছু মান সেট করে নিতে পারি। যেমনঃ

• কোন ভ্যারিয়েবলে মান সেট করতে একটা ইন্সট্রাকশন
• অ্যারের একটা ইনডেক্স থেকে ভ্যালু বের করতে একটা ইন্সট্রাকশন
• দুইটা ভ্যালুর মধ্যে তুলনা করতে একটা ইন্সট্রাকশন
• ইঙ্ক্রিমেন্ট(i++) অথবা ডিক্রিমেন্ট (i–) অপারেশন এর জন্য একটা ইন্সট্রাকশন ইত্যাদি।

এ হিসেবে ফর লুপের শুরুতে দুইটা ইন্সট্রাকশন লাগবে। শুরুতেই i = 0 এর জন্য একটা ইন্সট্রাকশন এবং i < n এর জন্য একটা ইন্সট্রাকশন। এই n এর মান হচ্ছে অ্যারেতে কয়টা ইলিমেন্ট রয়েছে, সে ভ্যালু। ধরে নিচ্ছি মিনিয়াম দুইটা ভ্যালু রয়েছে অ্যারেতে।

ফর লুপের প্রতিটি ইটারেশন শেষে আবার দুইটা ইন্সট্রাকশন লাগবে। একটা হচ্ছে i++ এর জন্য। এবং একটা i < n এর জন্য। লিস্টে যদি n টি ইলিমেন্ট থাকে, তাহলে 2n ইন্সট্রাকশন লাগবে।

ফর লুপের ভেতর আরো দুইটা ইন্সট্রাকশন। একটা হচ্ছে arr[i] ভ্যালু বের করা, আরেকটা হচ্ছে x এর সাথে তুলনা। লিস্টে যদি n টি ইলিমেন্ট থাকত, তাহলে এখানেও আমাদের 2n ইন্সট্রাকশন লাগবে।

সুতরাং আমাদের টোটাল ইন্সট্রাকশন লাগছেঃ 2 + 2n + 2n টি। আমরা যদি একটা ফাংশন চিন্তা করি, যেখানে n এর জন্য আমাদের অ্যালগরিদমটির কয়টা ইন্সট্রাকশন লাগবে, তাহলে আমরা পাবো f(n) = 2 + 2n + 2n = 2 + 4n

Best-case analysis:

ধরে নিচ্ছি আমাদের লিস্ট হচ্ছে arr=[4,3,6,8,1] আর আমরা বের করতে চাচ্ছি 4 এই লিস্টে রয়েছে কিনা। এখন আমরা যেহেতু লিনিয়ারলি সার্চ করছি, তাহলে আমরা শুরুতেই পেয়ে যাবো, 4 লিস্টে রয়েছে। তাহলে আমাদের ইন্সট্রাকশন লাগবে 2 + 2 বা চারটা। লুপের শুরুতেই দুইটা ইন্সট্রাকশন। এবং লুপের ভেতর দুইটা ইন্সট্রাকশন। এরপর লুপ থেকে বের হয়ে যাবে।

Worst-case analysis:

আমাদের লিস্ট যদি arr=[4,3,6,8,1] হয়, আর আমরা বের করতে চাচ্ছি 1 এই লিস্টে রয়েছে কিনা, তাহলে আমাদের ইন্সট্রাশন লাগবে অনেক বেশি। প্রতিটা নাম্বার একবার করে চেক করবে। একবারে শেষ ইলিমেন্টে এসে দেখবে 1 লিস্টে রয়েছে।

যে নাম্বারটি সার্চ করছি, তা লিস্টে না থাকলেও সব গুলো ইলিমেন্ট সার্চ করবে। যেমন আমরা যদি বের করতে চাই 5 লিস্টে রয়েছে কিনা, তাহলেও একই সময় লাগবে। প্রতিটা ইলিমেন্ট একবার করে দেখবে।

Asymptotic Notation:

লিনিয়ার সার্চের অ্যালগরিদমটি আমরা C তে ইমপ্লিমেন্ট করেছি। এখানে আমরা ফর লুপ ব্যবহার করেছি। ফর লুপ ব্যবহার করার জন্য আমাদের বাড়তি কিছু ইন্সট্রাকশন প্রসেস করতে হচ্ছে। অন্য কোন ল্যাঙ্গুয়েজে হয়তো আরো সহজেই এই প্রসেস গুলো করা যেতো আরো কম ইন্সট্রাকশনে। আবার যেহেতু এক এক প্রসেসরের প্রসেসিং ক্ষমতা এক এক রকম, তাই আমরা মাইনর বিষয় গুলো বাদ দিতে পারি।

এখন আমাদের ফাংশন f(n) = 2 + 4n এর দিকে তাকাই। n যদি অনেক বড় একটা সংখ্যা হয় যেমন এক ট্রিলিয়ন, তখন 2 তার তুলনায় নগণ্য। n এর ভ্যালু যাই হোক না কেন, 2 এর কোন পরিবর্তন হচ্ছে না। তাই আমরা এটিকে বাদ দিতে পারি। এখন থাকে 4n এখানে আমরা আবার 4 কে বাদ দিতে পারি কারণ এটিও কন্সট্যান্ট। তখন আমরা আমাদের লিনিয়ার সার্চের কমপ্লেক্সিটি ফাংশন f(n) কে লিখতে পারি f(n) = n;

জেনে রাখা দরকার  যে কোন প্রোগ্রামিং এ যদি ফর লুপ নিয়ে কাজ করে থাকি, তাহলে আমরা হয়তো জেনে থাকব একটা ফর লুপ ইটারেট করবে সর্বোচ্চ n বার। একটা ফরলুপের ভেতর আরেকটা ফরলুপ থাকতে তা ইটারেট করবে সর্বোচ্চ n*n বা n² বার। তিনটে ফরলুপ হলে সর্বোচ্চ n*n*n বা n³ বার ঘুরবে।

এখন যদি একটা অ্যালগরিদম এর ইন্সট্রাকশন কাউণ্ট করে আমরা পাই 8n + 5 তাহলে তাহলে তার Asymptotic Notation হবে n। 2n² + 8 এর Asymptotic Notation হবে n²। 4n³ + 9 এর Asymptotic Notation হবে n³

Asymptotic Notation কে সাধারণত লেখা হয় Θ(f(n)) যেমন আমাদের লিনিয়ার সার্চ অ্যালগরিদমের Asymptotic Notation Θ(n)। উচ্চারণ করা হয় theta of n।

Tight Bound: Asymptotic Notation এ একটা অ্যালগরিদম প্রসেস করতে কয়টা ইন্সট্রাকশন লাগবে, আমরা এক্সেক্টলি তত গুলোই ধরে নিচ্ছি। আর এ জন্য এটাকে বলা হয় Tight Bound। অর্থৎ আপনি যদি দেখেন কোন একটা অ্যালগরিদমের কমপ্লেক্সিটি Θ(n), তাহলে এই Θ(n) হচ্ছে ঐ অ্যালগরিদমের Tight Bound।

Big O Notation:

একটা অ্যালগরিদমের ইন্সট্রাকশন বা কমপ্লেক্সিটি ক্যালকুলেশন করে পেয়েছি f(n) = n। কিন্তু ইমপ্লিমেন্ট করতে গিয়ে দেখা গেলো ঐ অ্যালগরিদম রান করতে n² টি ইন্সট্রাকশন লাগে বা লাগতে পারে। তাহলে এই n² কে বলা হয় ঐ অ্যালগরিদমের Upper Bound. আর এটিকে Big O Notation দিয়ে প্রকাশ করা হয়। আমরা সাধারণত worst case নিয়ে চিন্তা করি। তাই কোন অ্যালগরিদমের কমপ্লিক্সিটি সাধারণত Big O Notaion দিয়েই প্রকাশ করা হয়।

বিভিন্ন ধরনের কমপ্লেক্সিটিঃ

O(n) বা Linear complexity: ইনপুট আইটেম (n) এর মান বাড়ার সাথে সাথে ইন্সট্রাকশন লিনিয়ারলি বাড়ে। যেমনঃ

• 1 item: 1 instruction
• 10 items: 10 instructions
• 100 items: 100 instructions

O(n²) বা Quadratic complexity: ইনপুট আইটেম n হলে ইন্সট্রাকশন লাগতে পারে n²। যেমনঃ

– 1 item: 1 instraction
– 10 items: 100 instructions
– 100 items: 10000 instructions

O(1) বা Constant complexity: ইনপুট যাই হোক না কেন, সব সময় কনস্ট্যান্ট ইন্সট্রাকশনই লাগবে। যেমনঃ

• 1 item: 1 instruction
• 10 items: 1 instructions
• 100 items: 1 instructions

O(log n) বা Logarithmic complexity: ইনপুট আইটেম বাড়ার সাথে সাথে ইন্সট্রাকশন লগারিদমিক আকারে বাড়বে। যেমনঃ

• 1 item: 1 instruction
• 10 items: 2 instructions
• 100 items: 3 instructions
• 1000 items: 4 instructions
• 10000 items: 5 instructions

একটা অ্যালগরিদমের পারফর্মনেস নির্ণয়ে নিচের বিষয় গুলো সাধারণত দেখা হয়ঃ

• Completeness
• Optimal or not
• Time Complexity
• Space Complexity

একটা সমস্যার জন্য আমরা কোন অ্যালগরিদমটা ব্যবহার করব, তা নির্নয় করার জন্য উপরের বিষয় গুলো আমরা দেখতে পারি। কমপ্লিটনেস মানে আমাদের অ্যালগরিদমটা কি সলিউশন দিবে কিনা। কত সময় লাগবে, কত মেমরি লাগবে ইত্যাদি।

 

এই সম্পর্কিত আরো কিছু লেখাঃ

• অ্যালগরিদমঃ লিনিয়ার সার্চ
• অ্যালগরিদমঃ বাবল সর্ট
• ব্রেডথ ফার্স্ট সার্চ অ্যালগরিদম – Breadth-first search
• ডেপথ ফার্স্ট সার্চ অ্যালগরিদম – Depth-First Search
• রিকার্শন/ Recursion , রিকার্সিভ অ্যালগরিদম, রিকার্সিভ ফাংশন ও সি প্রোগ্রামিং এ প্রয়োগ
• লিঙ্কড লিস্ট / Linked list সম্পর্কে ধারণা এবং সি প্রোগ্রামিং এ ইমপ্লিমেন্টেশন
• গ্রাফ থিওরি, গ্রাফের রিপ্রেজেন্টেশন এবং ইমপ্লিমেন্টেশন